
Những câu hỏi liên quan
Cho góc nhọn xOy. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B, trên tia phân giác của góc xOy lấy điểm M sao cho OA=OB=OM. Chứng minh rằng tam giác AMB cân.
Xét tam giác OMA và tam giác OMB ,có :
OM chung
góc O1 = góc O2 ( gt )
OA = OB ( gt )
=> tam giác OMA = tam giác OMB ( c-g-c )
=> MA = MB ( hai cạnh tương ứng )
=> tam giác AMB cân tại A
Vậy tam giác AMB cân
Đúng 0
Bình luận (0)
Cho góc xOy nhọn. Lấy điểm A trên tia Ox, điểm B trên tia Oy. Trên tia Ox lấy điểm C sao cho BC là tia phân giác của góc ABy. Gọi I là giao điểm của hai tia phân giác góc xAB và xOy. Chứng minh ba điểm B, I, C thẳng hàng.
Góc AIB = 180 độ - 1/2 BAC - ABI
Góc AIC = 180 độ - 1/2 BAC - ACI
⇒ AIB + AIC = 180 độ - BAC - (ABI + ACI)
Giả sử B, I, C thẳng hàng
⇒BIC = 180 độ = AIB + AIC
→360 độ - BAC - (ABI + ACI) = 180 độ
ABI + ACI = 180 độ - BAC (LĐ)
Vậy điều giả sử là đúng
⇒B, I, C thẳng hàng
Đúng 0
Bình luận (0)
Bài 7. Cho góc xOy nhọn. Lấy điểm A trên tia Ox, điểm B trên tia Oy. Trên tia Ox lấy điểm C sao cho BC là tia phân giác của góc ABy. Gọi I là giao điểm của hai tia phân giác góc xAB và xOy. Chứng minh ba điểm B, I, C thẳng hàng
Câu hỏi:
Cho góc nhọn xOy. trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA=OB. Trên tia Ox lấy điểm C, trên tia Oy lấy điểm D sao cho OC=OD.
a) Chứng minh: AD=BC
b) Gọi E là giao điểm AD và BC. Chứng minh: OE là tia phân giác của góc xOy.
(Kèm thêm vẽ hình nữa nhé các bạn)
Cho góc nhọn xOy,trên tia Ox lấy điểm A, Trên Oy lấy điểm B và C sao cho OA = BC. Các đường trung trực của các đoạn thẳng AB và OC cắt nhau tại D. Chứng minh OD là phân giác của góc xOy
Cho góc nhọn xOy. Trên tia Ox lấy điểm A, Trên tia Oy lấy điểm B sao cho OA=OB. Trên tia Ax lấy điểm C, trên tia By lấy điểm D sao cho OC=OD
a) Chứng minh: AD=BC
b) Gọi E là giao điểm AD và BC.Chứng minh:OE là tia phân giác của góc xOy
Xem chi tiết
Mn giải giúp em với ạ
Bài 2. Cho góc xAy. Lấy điểm B trên Ax, điểm D trên Ay sao cho AB AD. Trên tia Bx lấy điểm E, trên tia Dy lấy điểm C sao cho BE DC. Chứng minh AABC AADEBài 3. Cho góc nhọn xOy và tia Oz là tia phân giác của góc xOy. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA OB. Lấy điểm I thuộc tia Oz Chứng minh rằng a) AAOI ABOI b) AB 1 OIBài 4. Cho tam giác ABC vuông tại A. Trên tia đối của tia AC lấy điểm D sao cho AD AC a) Chứng minh ABAC ABAD b) Trên tia đối của tia AB lấy điểm M. Chứ...
Đọc tiếp
Bài 2. Cho góc xAy. Lấy điểm B trên Ax, điểm D trên Ay sao cho AB = AD. Trên tia Bx lấy điểm E, trên tia Dy lấy điểm C sao cho BE = DC. Chứng minh AABC = AADE
Bài 3. Cho góc nhọn xOy và tia Oz là tia phân giác của góc xOy. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA = OB. Lấy điểm I thuộc tia Oz Chứng minh rằng a) AAOI = ABOI b) AB 1 OI
Bài 4. Cho tam giác ABC vuông tại A. Trên tia đối của tia AC lấy điểm D sao cho AD = AC a) Chứng minh ABAC = ABAD b) Trên tia đối của tia AB lấy điểm M. Chứng minh AMBD = AMBC
Bài 4:
a: Xét ΔABC vuông tại A và ΔABD vuông tại A có
BA chung
AC=AD
Do đó: ΔABC=ΔABD
b: Xét ΔMAC vuông tại A và ΔMAD vuông tại A có
MA chung
AC=AD
Do đó: ΔMAC=ΔMAD
Xét ΔMBD và ΔMBC có
MB chung
BD=BC
MD=MC
Do đó: ΔMBD=ΔMBC
Đúng 1
Bình luận (0)
cho góc nhọn xOy và tia phân giác Oz của góc đó .Trên tia Ox lấy điểm a ,trên tia Oy lấy điểm b sao cho oa=ob . trên tia Oz lấy điểm I bất kì chứng minh a) tam giác AOI = tam giác BOI
B) AB VUÔNG GÓC OI
Ta có hình vẽ:
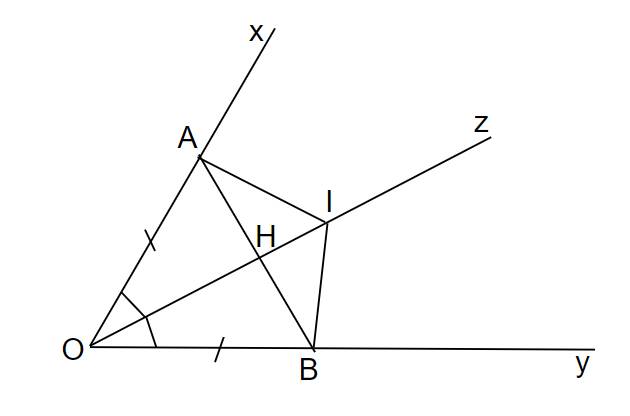
a) Vì Oz là phân giác của xOy nên
Xét Δ AOI và Δ BOI có:
OA = OB (gt)
AOI = BOI (cmt)
OI là cạnh chung
Do đó, Δ AOI = Δ BOI (c.g.c) (đpcm)
b) Xét Δ AOH và Δ BOH có:
OA = OB (gt)
AOH = BOH (câu a)
OH là cạnh chung
Do đó, Δ AOH = Δ BOH (c.g.c)
=> AHO = BHO (2 góc tương ứng)
Mà AHO + BHO = 180o (kề bù) nên AHO = BHO = 90o
=>
Đúng 0
Bình luận (0)
Cho góc xOy nhọn, trên Ox lấy điểm A, trên Oy lấy điểm B.Vẽ tia At và Bz sao cho xAt+yBz=xOy. CMR: At//Bz
Bài 1. Cho góc xOy nhọn. Kẻ tia phân giác Ot của góc xOy. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA OB. Từ A kẻ đường thẳng vuông góc với tia Ox và cắt tia Ot tại C.a) Chứng minh tam giác AOC tam giác BOC.b) Chứng minh CB I Oy.c) Chứng minh OC là đường trung trực của đoạn thẳng AB.d) Kẻ BI | Ox tại I, BI cắt OC tại H. Kẻ HK I Oy tại K. Chứng minh 3 điểm A, H, K thẳng hàng.e) Giả sử góc xOy 60° và OH 3m. Tính khoảng cách từ điểm H tới hai cạnh Ox và Oy.
Đọc tiếp
Bài 1. Cho góc xOy nhọn. Kẻ tia phân giác Ot của góc xOy. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA = OB. Từ A kẻ đường thẳng vuông góc với tia Ox và cắt tia Ot tại C.
a) Chứng minh tam giác AOC = tam giác BOC.
b) Chứng minh CB I Oy.
c) Chứng minh OC là đường trung trực của đoạn thẳng AB.
d) Kẻ BI | Ox tại I, BI cắt OC tại H. Kẻ HK I Oy tại K. Chứng minh 3 điểm A, H, K thẳng hàng.
e) Giả sử góc xOy = 60° và OH = 3m. Tính khoảng cách từ điểm H tới hai cạnh Ox và Oy.
a: Xét ΔOAC và ΔOBC có
OA=OB
góc AOC=góc BOC
OC chung
=>ΔOAC=ΔOBC
b: ΔOAC=ΔOBC
=>góc OBC=90 độ
=>CB vuông góc Oy
c: OA=OB
CA=CB
=>OC là trung trực của AB
Đúng 0
Bình luận (0)


















