Tập hợp các số hữu tỉ là gì?

Những câu hỏi liên quan
Biểu đồ minh họa trong hình nói gì về quan hệ giữa tập hợp các số nguyên Z và tập hợp các số hữu tỉ Q ? Có thể nói mỗi số nguyên là một số hữu tỉ hay không?
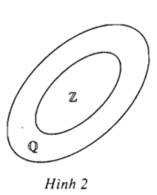
Tập hợp các số nguyên Z nằm trong tập hợp các số hữu tỉ Q
Có thể nói mỗi số nguyên là một số hữu tỉ
Đúng 0
Bình luận (0)
Thế nào là trục số thực, mối quan hệ giữa các tập hợp số tự nhiên, số nguyên,số hữu tỉ,số vô tỉ và số thực là gì?
tập hợp số hữu tỉ là gì
Trong toán học, số hữu tỉ là các số x có thể biểu diễn dưới dạng phân số(thương) a/b, trong đó a và b là các số nguyên nhưng b0. Tập hợp số hữu tỉ kí hiệu là
\(Q=\left\{X\left|X\right|=\frac{M}{N};m\in Z,n\in Z^{\cdot}\right\}\)
Tập hợp số hữu tỉ là tập hợp đếm được.
Các số thực không phải là số hữu tỷ được gọi là các số vô tỷ.
Tuy nhiên, tập hợp các số hữu tỷ không hoàn toàn đồng nhất với tập hợp các phân số p/q,vì mỗi số hữu tỷ có thể biểu diễn bằng nhiều phân số khác nhau. Chẳng hạn các phân số 1/3,2/6,3/9... cùng biểu diễn một số hữu tỷ.
Đúng 0
Bình luận (0)
Tập hợp các số hữu tỉ được kí hiệu là gì ?
Trả lời xong nhớ kb nha !
Xem thêm câu trả lời
Các mệnh đề sau đúng hay sai?
a) Mọi số nguyên đều viết được dưới dạng phân số
b) Tập hợp các số thực chứa tập hợp các số hữu tỉ;
c) Tồn tại một số thực không là số hữu tỉ.
a) Mệnh đề “Mọi số nguyên đều viết được dưới dạng phân số” đúng.
Vì \(\forall a \in \mathbb{Z}:a = \dfrac{a}{1}\)
Hoặc: \(a \in \mathbb{Z} \subset \mathbb{Q}\) => mỗi số nguyên cũng là một phân số.
b) Mệnh đề "Tập hợp các số thực chứa tập hợp các số hữu tỉ" là mệnh đề đúng.
c) Mệnh đề “Tồn tại một số thực không là số hữu tỉ” đúng.
Ví dụ: \(\sqrt 2 \) ( vì \(\sqrt 2 \in \mathbb{R};\;\sqrt 2 \notin \mathbb{Q}\)).
Đúng 0
Bình luận (0)
Câu 2. Trong các câu sau, câu nào đúng? A. Số hữu tỉ âm nhỏ hơn số hữu tỉ dương. B. Số 0 là số hữu tỉ dương. C. Số nguyên âm không phải là số hữu tỉ âm. D. Tập hợp gồm các số hữu tỉ dương và các số hữu tỉ âm.Giai thich :)))
Đọc tiếp
Câu 2. Trong các câu sau, câu nào đúng?
A. Số hữu tỉ âm nhỏ hơn số hữu tỉ dương.
B. Số 0 là số hữu tỉ dương.
C. Số nguyên âm không phải là số hữu tỉ âm.
D. Tập hợp gồm các số hữu tỉ dương và các số hữu tỉ âm.
Giai thich :)))
`#3107.101107`
2.
A. Số hữu tỉ âm nhỏ hơn số hữu tỉ dương - Đúng
Vì số hữu tỉ âm nằm bên trái của trục số thực và bé hơn 0
B. Số 0 là số hữu tỉ dương - Sai
Số 0 không phải là số hữu tỉ dương cũng không phải là số hữu tỉ âm
C. Số nguyên âm không phải số hữu tỉ âm - Sai
Các số nguyên âm x có thể được viết dưới dạng `x/1`, do đó số nguyên âm cũng là số hữu tỉ âm
D. Tập hợp Q gồm các số hữu tỉ dương và các số hữu tỉ âm? - Sai
Tập hợp Q bao gồm các số hữu tỉ âm, dương và cả số 0.
`=>` Chọn đáp án A.
Đúng 1
Bình luận (0)
Trong các câu sau câu nào đúng câu nào sai”
a. Số hữu tỉ âm nhỏ hơn số hữu tỉ dương
b. Số hữu tỉ âm nhỏ hơn số tự nhiên
c. Số 0 là số hữu tỉ dương
d. Số nguyên âm không phải là số hữu tỉ âm
e. Tập hợp Q gồm các số hữu tỉ dương và các số hữu tỉ âm
a. Số hữu tỉ âm nhỏ hơn số hữu tỉ dương. Đúng
b. Số hữu tỉ âm nhỏ hơn số tự nhiên. Đúng
c. Số 0 là số hữu tỉ dương. Sai
Vì số 0 không là số hữu tỉ dương cũng không là số hữu tỉ âm.
d. Số nguyên âm không phải là số hữu tỉ âm. Sai
Các số nguyên âm a luôn viết được dưới dạng: 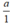 . Do đó, số nguyên âm có là số hữu tỉ âm.
. Do đó, số nguyên âm có là số hữu tỉ âm.
e. Tập hợp Q gồm các số hữu tỉ dương và các số hữu tỉ âm. Sai
Vì tập hợp Q gồm các số hữu tỉ dương, các số hữu tỉ âm và số 0.
Đúng 1
Bình luận (0)
1. Cho các số hữu tỉ .
a/ Hãy so sánh các số hữu tỉ đó .
b/ Viết tập hợp các số hữu tỉ bằng các số hữu tỉ trên .
Chỉ mình tập hợp hữu hạn là gì ?là một tập hợp có một số hữu hạn các phần tử ( ý của cái này nghĩa là gì ạ mình chứa hiểu ) . Lấy ví dụ nhá
Trong toán học, một tập hợp hữu hạn là một tập hợp có một số hữu hạn các phần tử. Một cách không chính thức, một tập hữu hạn là một tập hợp mà có thể đếm và có thể kết thúc việc đếm. Ví dụ,
là một tập hợp hữu hạn có 5 phần tử. Số phần tử của một tập hợp hữu hạn là một số tự nhiên (một số nguyên không âm) và được gọi là lực lượng của tập hợp đó. Một tập hợp mà không hữu hạn được gọi là tập hợp vô hạn. Ví dụ, tập hợp tất cả các số nguyên dương là vô hạn:
Tập hợp hữu hạn đặc biệt quan trọng trong toán học tổ hợp, môn toán học nghiên cứu về phép đếm. Nhiều bài toán liên quan đến các tập hữu hạn dựa vào nguyên lý ngăn kéo Dirichlet, chỉ ra rằng không thể tồn tại một đơn ánh từ một tập hợp hữu hạn lớn hơn vào một tập hợp hữu hạn nhỏ hơn.
Đúng 0
Bình luận (1)
Tham khảo:
Trong toán học, một tập hợp hữu hạn là một tập hợp có một số hữu hạn các phần tử. Một cách không chính thức, một tập hữu hạn là một tập hợp mà có thể đếm và có thể kết thúc việc đếm
Đúng 0
Bình luận (0)

























