Ta có:

\(x^3+x^2z-xyz+y^2z+y^3\)

\(=\left(x^3+y^3\right)+\left(x^2z-xyz+y^2z\right)\)

\(=\left(x+y\right)\left(x^2-xy+y^2\right)+z\left(x^2-xy+y^2\right)\)

\(=\left(x+y+z\right)\left(x^2-xy+y^2\right)\)

\(=0\cdot\left(x^2-xy+y^2\right)\)

\(=0\left(dpcm\right)\)

Với x ≥ 0; y ≥ 0 thì x + y ≥ 0

Ta có: x3 + y3 ≥ x2y + xy2

⇔ (x3 + y3) – (x2y + xy2) ≥ 0

⇔ (x + y)(x2 – xy + y2) – xy(x + y) ≥ 0

⇔ (x + y)(x2 – xy + y2 – xy) ≥ 0

⇔ (x + y)(x2 – 2xy + y2) ≥ 0

⇔ (x + y)(x – y)2 ≥ 0 (Luôn đúng vì x + y ≥ 0 ; (x – y)2 ≥ 0)

Dấu « = » xảy ra khi (x – y)2 = 0 ⇔ x = y.

(x³+x²y+xy²+y³)(x-y)

=x(x³+x²y+xy²+y³)-y(x³+x²y+xy²+y³)

=x⁴+x³y+x²y²+xy³-x³y-x²y²+xy³+y⁴

= x⁴+y⁴

đề sai bạn xem lại đề

*) Từ x > y > 0 ta có:

x > y ⇒ xy > y2     (1)

x > y ⇒ x2 > xy     (2)

*) Từ (1) và ( 2 ) suy ra x2 > y2.

x2 > y2 ⇒ x3 > xy2 (3)

x > y ⇒ xy2 > y3 (4)

Từ (3) và (4) suy ra x3 > y3.

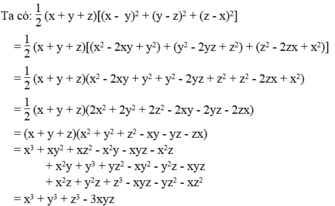
Vế trái bằng vế phải nên đẳng thức được chứng minh.

Nếu x ≥ 0, y  ≥  0, z  ≥  0 thì:

x + y + z  ≥  0

x - y 2 + y - z 2 + z - x 2 ≥ 0

Suy ra:

x 3 + y 3 + z 3 - 3 x y z ≥ 0 ⇔ x 3 + y 3 + z 3 ≥ 3 x y z

Hay:  x 3 + y 3 + z 3 3 ≥ x y z

CMR: \(\frac{1}{x}+\frac{1}{y}\le2\)  biết \(^{x^3+y^3+3\left(x^2+y^2\right)+4\left(x+y\right)+4=0}\) và xy>0

tôi quên mât CMR: 1/x+1/y<=-2