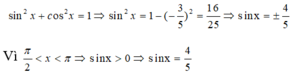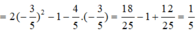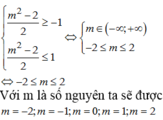Cho góc x, với cosx . Tính giá trị của biểu thức : P 3sin2x +cos2x.
Đọc tiếp
Cho góc x, với cosx = . Tính giá trị của biểu thức : P = 3sin2x +cos2x.
Những câu hỏi liên quan
Cho góc x, với cosx = 1/3. Tính giá trị của biểu thức: P = 3sin2x + cos2x.
Ta có : sin2 x + cos2 x = 1 ⇒ sin2 x = 1 – cos2 x.
⇒ P = 3.sin2 x + cos2 x
= 3.(1 – cos2x) + cos2 x
= 3 – 3.cos2x + cos2x
= 3 – 2.cos2x
= 3 – 2.(1/3)2
= 3 – 2/9
= 25/9.
Đúng 1
Bình luận (0)
Cho cos x = 3 5 , ( π 2 < x < π )
Tính giá trị biểu thức sau:
P = cos 2 x - 1 2 sin 2 x
Có bao nhiêu giá trị nguyên của tham số m để phương trình
cos
2
x
-
3
sin
2
x
-
2
3
sin
x
+
cos
x
+
m
0
có nghiệm
x
∈
-
π
3...
Đọc tiếp
Có bao nhiêu giá trị nguyên của tham số m để phương trình cos 2 x - 3 sin 2 x - 2 3 sin x + cos x + m = 0 có nghiệm x ∈ - π 3 ; 2 π 3
A. 4
B. 3
C. 9
D. 10
Chọn đáp án C
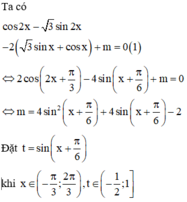
Bảng biến thiên:
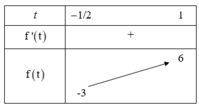
Từ bảng biến thiên ta có phương trình (1) đã cho có nghiệm
Vậy có 9 giá trị nguyên của m thỏa mãn yêu cầu bài toán.
Đúng 0
Bình luận (0)
Cho góc x, với cosx = 2/3. Tính giá trị của biểu thức: P = 5sin2x + 2cos2x.
A. 22/9
B. 8/3
C. 33/9
D. 1
Chọn C.
Ta có: sin2x + cos2x = 1 ⇒ sin2x = 1 – cos2x = 1 – 4/9 = 5/9
Vậy: 
Đúng 0
Bình luận (0)
15 tháng 12 2023 lúc 13:05
1. Cho biết \(cosx=\dfrac{3}{4}\). Tính giá trị của biểu thức \(P=sin^22x\).
2. Giải phương trình \(cos2x-sin\left(x+\dfrac{\pi}{3}\right)=0\)
1: \(P=sin^22x=1-cos^22x\)
\(=1-\left(cos2x\right)^2\)
\(=1-\left(2cos^2x-1\right)^2\)
\(=1-\left(2\cdot\dfrac{9}{16}-1\right)^2\)
\(=1-\left(\dfrac{9}{8}-1\right)^2=1-\left(\dfrac{1}{8}\right)^2=\dfrac{63}{64}\)
2:
\(cos2x-sin\left(x+\dfrac{\Omega}{3}\right)=0\)
=>\(sin\left(x+\dfrac{\Omega}{3}\right)=cos2x=sin\left(\dfrac{\Omega}{2}-2x\right)\)
=>\(\left[{}\begin{matrix}x+\dfrac{\Omega}{3}=\dfrac{\Omega}{2}-2x+k2\Omega\\x+\dfrac{\Omega}{3}=\Omega-\dfrac{\Omega}{2}+2x+k2\Omega\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}3x=\dfrac{\Omega}{6}+k2\Omega\\-x=\dfrac{1}{6}\Omega+k2\Omega\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\Omega}{18}+\dfrac{k2\Omega}{3}\\x=-\dfrac{1}{6}\Omega-k2\Omega\end{matrix}\right.\)
Đúng 0
Bình luận (0)
tính giá trị biểu thức P bằng sin2-sinx*cosx+2cos2x/2sin2x-cos2x biết tan x bằng 3
Lần sau bạn vào cái hình E để gửi câu hỏi nha!
\(P=\dfrac{sin^2\alpha-sin\alpha\cdot cos\alpha+2cos^2\alpha}{2sin^2\alpha-cos^2\alpha}\)
\(P=\dfrac{tan^2\alpha-tan\alpha+2}{2tan^2\alpha-1}\) (Chia cả tử và mẫu cho \(cos^2\alpha\))
\(P=\dfrac{3^2-3+2}{2\cdot3^2-1}=\dfrac{8}{17}\)
Chúc bn học tốt!
Đúng 1
Bình luận (0)
Tìm góc
α
∈
π
6
;
π
4
;
π
3
;
π
2
để phương trình
cos
2
x
+
3
sin
2
x
−
2
cos...
Đọc tiếp
Tìm góc α ∈ π 6 ; π 4 ; π 3 ; π 2 để phương trình cos 2 x + 3 sin 2 x − 2 cos x = 0 tương đương với phương trình cos 2 x − α = cos x
A. α = π 3
B. α = π 4
C. α = π 6
D. α = π 2
Đáp án A
Ta có
cos 2 x + 3 sin 2 x − 2 cos x = 0 ⇔ sin 2 x + π 6 = cos x ⇔ cos 2 x − π 3 = cos x
Suy ra cos 2 x − π 3 = cos x ⇔ cos 2 x − α = cos x ⇔ α = π 3
Đúng 0
Bình luận (0)
Có bao nhiêu giá trị nguyên m để phương trình dưới đây có nghiệm?
4
sin
x
+
π
3
.
cos
x
-
π
6
m
2
+
3
sin
2
x
-
cos
2
x
A. ...
Đọc tiếp
Có bao nhiêu giá trị nguyên m để phương trình dưới đây có nghiệm?
4 sin x + π 3 . cos x - π 6 = m 2 + 3 sin 2 x - cos 2 x
A. 7.
B. 1
C. 3.
D. 5.
Có bao nhiêu giá trị nguyên m để phương trình dưới đây có nghiệm?
4
sin
x
+
π
3
.
cos
x
-
π
6
m
2
+
3
sin
2
x
-
cos
2
x...
Đọc tiếp
Có bao nhiêu giá trị nguyên m để phương trình dưới đây có nghiệm? 4 sin x + π 3 . cos x - π 6 = m 2 + 3 sin 2 x - cos 2 x
A. 7
B. 1
C. 3
D. 5
Cho biết cotx 1/2. Giá trị biểu thức A
2
sin
2
x
-
sin
x
.
cos
x
-
cos
2
x
bằng A. 6. B. 8. C. 10. D. 12.
Đọc tiếp
Cho biết cotx = 1/2. Giá trị biểu thức A= 2 sin 2 x - sin x . cos x - cos 2 x bằng
A. 6.
B. 8.
C. 10.
D. 12.
Chọn C.
Chia cả tử và mẫu cho sin2x ta được
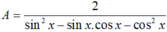
Đúng 0
Bình luận (0)