tìm các số nguyên tố a và b, biết a2-2b2-1=0
Những câu hỏi liên quan
Biết rằng tồn tại các số nguyên a, b sao cho hàm số
y
a
x
+
b
x
2
+
1
đạt giá trị nhỏ nhất, giá trị lớn nhất đều là các số nguyên và tập giá trị của hàm số đã cho chỉ có đúng 6 số nguyên. Giá trị của
a
2
+
2
b...
Đọc tiếp
Biết rằng tồn tại các số nguyên a, b sao cho hàm số y = a x + b x 2 + 1 đạt giá trị nhỏ nhất, giá trị lớn nhất đều là các số nguyên và tập giá trị của hàm số đã cho chỉ có đúng 6 số nguyên. Giá trị của a 2 + 2 b 2 bằng
A. 36
B. 34
C. 41
D. 25
Chọn đáp án B.
Bằng cách sử dụng điều kiện tồn tại nghiệm của phương trình, chúng ta có: Khi a = 0 thì hàm số chỉ đạt giá trị lớn nhất (khi b < 0) hoặc chỉ đạt giá trị nhỏ nhất (khi b > 0). Còn khi
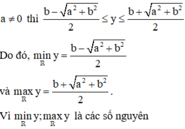
nên tập giá trị của hàm số đã cho chỉ có đúng 6 số nguyên khi và chỉ khi
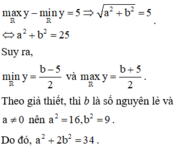
Đúng 0
Bình luận (0)
cho a,b là các số nguyên dương thỏa mãn a2-ab+3/2b2 chia hết cho 25. Chứng minh rằng cả a và b đều chia hết cho 5.
cho a, b là hai số nguyên phân biệt lớn hơn 1 thỏa mãn a+2b2 - 2 là lũy thừa của một số nguyên tố khác 13, và b+2a2-2 chia hết cho a+2b2 - 2 chứng minh răng 2a+3 là số chính phươngcho a, b là hai số nguyên phân biệt lớn hơn 1 thỏa mãn a+2b2 - 2 là lũy thừa của một số nguyên tố khác 13, và b+2a2-2 chia hết cho a+2b2 - 2 chứng minh răng 2a+3 là số chính phương
Đọc tiếp
cho a, b là hai số nguyên phân biệt lớn hơn 1 thỏa mãn a+2b2 - 2 là lũy thừa của một số nguyên tố khác 13, và b+2a2-2 chia hết cho a+2b2 - 2 chứng minh răng 2a+3 là số chính phươngcho a, b là hai số nguyên phân biệt lớn hơn 1 thỏa mãn a+2b2 - 2 là lũy thừa của một số nguyên tố khác 13, và b+2a2-2 chia hết cho a+2b2 - 2 chứng minh răng 2a+3 là số chính phương
26 tháng 12 2023 lúc 19:08
Cho a;b;c là các số nguyên tố . Tìm a;b;c , biết :
a2 + b2 + c2 = 5070
Lời giải:
Không mất tổng quát giả sử $a\leq b\leq c$
Nếu $a,b,c$ đều là số nguyên tố lẻ thì $a^2+b^2+c^2$ là số lẻ. Mà $5070$ chẵn nên vô lý.
Do đó trong 3 số $a,b,c$ tồn tại ít nhất 1 số chẵn.
Số nguyên tố chẵn luôn là số bé nhất (2) nên $a=2$
Khi đó: $b^2+c^2=5070-a^2=5066\geq 2b^2$
$\Rightarrow b^2\leq 2533$
$\Rightarrow b< 51$
$\Rightarrow b\in \left\{2; 3; 5; 7; 11; 13; 17; 19; 23; 29; 31; 37; 41; 43; 47\right\}$
Thử các TH này ta thấy $(b,c)=(5,71), (29,65)$
Vậy $(a,b,c)=(2,5,71), (2,29,65)$ và các hoán vị.
Đúng 1
Bình luận (0)
vì 5070 là số chẵn ⇒ một trong 3 số a,b,c chẵn hoặc cả 3 số a,b,c chẵn
+) cả 3 số a,b,c chẵn
=> a=2, b=2, c=2 ( vì a,b,c là các số nguyên tố )
khi đó: a2+b2+c2= 12(loại)
=> một trong 3 số a,b,c chẵn
vì giá trị các số bằng nhau, giả sử a chẵn => a=2
khi đó: a2+b2+c2= 4+b2+c2
=> b2+c2= 5066
vì số chính phương có tận cùng là 0, 1, 4, 5, 6, 9 mà b2 và c2 là số chính phương có tận cùng là 0, 1, 4, 5, 6, 9
=> b2 và c2 có tận cùng là 0, 1, 4, 5, 6, 9
Mà b và c lẻ
=> b2 và c2 có tận cùng là 1, 5, 9
mà 5066 có tận cùng là 6
=> b2 và c2 có tận cùng là 1, 5
=> b và c có tận cùng là 1, 5
giả sử b có tận cùng là 5=> b=5
khi đó: 25+ c2 = 5066
c2 = 5041=712
=> c = 71
vậy, a=2, b=5, c=71 và các hoán vị của nó
Đúng 0
Bình luận (0)
b. Tìm các số nguyên a thỏa mãn: (a2 + 1)(a2 - 2)(a2 -5) < 0.
Cho số Nguyên tố a;b;c ; cho các stn m khác 0 . sao cho a2+b2+25c2=9m2+1
Mô tả thuật toán bằng 2 cách ( liệt kê các bước và sơ đồ khối) các thuật toán đưa ra để máy tính chạy đc:1, tìm ước của số nguyên a2, tìm ƯCLN và BCNN của 2 số nguyên a và b3, ktra số nguyên a có là số nguyên tố hay ko?4, rút gọn phân số a/b 5, ktra 3 số a,b,c có là 3 cạnh của tam giác hay ko?
Đọc tiếp
Mô tả thuật toán bằng 2 cách ( liệt kê các bước và sơ đồ khối) các thuật toán đưa ra để máy tính chạy đc:
1, tìm ước của số nguyên a
2, tìm ƯCLN và BCNN của 2 số nguyên a và b
3, ktra số nguyên a có là số nguyên tố hay ko?
4, rút gọn phân số a/b
5, ktra 3 số a,b,c có là 3 cạnh của tam giác hay ko?
1)a)tìm n thuộc N*để 3n+1chia hết cho5n-2b)tìm các chữ số a,,b,c để 7268abc chia hết cho 7,12,8,92)cho a và blaf 2 số nguyên tố cùng nhau sao cho a,b khác tính chẵn lẻ cmr a+b và a(a+2)+ab là 2 số nguyên tố cùng nhau3)cmr với mọi n thuộc N* thì1.2.3+2.3.5+3.4.7+..+n(n+1)(2n+1)n(n+1)^2(n+2)/24)cho 17 số tự nhiên khác 0:a1,a2,a3,....,a17mà a1+a2+a3+...+a17153153cmr a1^5+a2^9+a3^13+...+a17^69 không phải số chính phương
Đọc tiếp
1)a)tìm n thuộc N*để 3n+1chia hết cho5n-2
b)tìm các chữ số a,,b,c để 7268abc chia hết cho 7,12,8,9
2)cho a và blaf 2 số nguyên tố cùng nhau sao cho a,b khác tính chẵn lẻ cmr a+b và a(a+2)+ab là 2 số nguyên tố cùng nhau
3)cmr với mọi n thuộc N* thì
1.2.3+2.3.5+3.4.7+..+n(n+1)(2n+1)=n(n+1)^2(n+2)/2
4)cho 17 số tự nhiên khác 0:a1,a2,a3,....,a17mà a1+a2+a3+...+a17=153153
cmr a1^5+a2^9+a3^13+...+a17^69 không phải số chính phương
ai muốn kết bn với tớ thì hãy click cho tớ nhé
Đúng 0
Bình luận (0)
22 tháng 5 2022 lúc 19:41
cho 3 số thực dương không âm thỏa mãn a+b+c1
tìm MAX của P√a2+2b2+√b2+2c2+√c2+2a2
Đọc tiếp
cho 3 số thực dương không âm thỏa mãn a+b+c=1
tìm MAX của
Dấu "=" xảy ra khi và các hoán vị
Đúng 2
Bình luận (0)