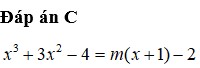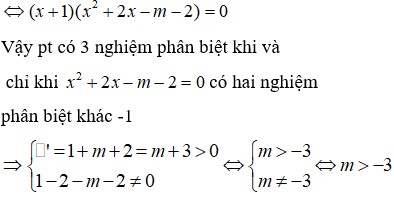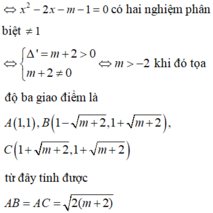Cho y= -x3 + 3x2 - 2 .tìm m để y = m(2-x) +2 cắt (c) tại 3 điểm phân biệt A(2;2) ,B,C sao cho tích các hệ số góc tiếp tuyến của (C) tại B , C đạt GTNN

Những câu hỏi liên quan
Tìm m để đường thẳng y=m(x+1)-2 cắt đồ thị hàm số y = x 3 + 3 x 2 - 4 tại ba điểm phân biệt
A. m>3
B. m<3
C. m>-3
D. m<-3
Tìm tất cả các giá trị thực của tham số m để đường thẳng
y
m
x
−
m
+
1
cắt đồ thị hàm số
y
x
3
−
3
x
2
+
x
+
2
tại ba điểm phân biệt A, B, C sao cho ABBC. A.
m
∈
−
∞
;...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để đường thẳng y = m x − m + 1 cắt đồ thị hàm số y = x 3 − 3 x 2 + x + 2 tại ba điểm phân biệt A, B, C sao cho AB=BC.
A. m ∈ − ∞ ; 0 ∪ 4 ; + ∞
B. m ∈ ℝ
C. m ∈ − 5 4 ; + ∞
D. m ∈ − 2 ; + ∞
Tìm m để
(
C
1
)
:
y
3
x
2
-
x
3
và
(
C
2
)
:
y
x
3
+
m
cắt nhau tại 3 điểm phân biệt.
Đọc tiếp
Tìm m để ( C 1 ) : y = 3 x 2 - x 3 và ( C 2 ) : y = x 3 + m cắt nhau tại 3 điểm phân biệt.
![]()
![]()
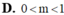
Tìm m để đường thẳng y = m x + 1 - 2 cắt đồ thị hàm số y = x 3 + 3 x 2 - 4 tại ba điểm phân biệt.
A. m > 3
B. m < 3
C. m > -3
D. m < -3
Tìm m để đường thẳng
y
m
x
+
1
-
2
cắt đồ thị hàm số
y
x
3
+
3
x
2
-
4
tại ba điểm phân biệt. A.
m
3
B.
m
3
C.
m
-
3
D. ...
Đọc tiếp
Tìm m để đường thẳng y = m x + 1 - 2 cắt đồ thị hàm số y = x 3 + 3 x 2 - 4 tại ba điểm phân biệt.
A. m > 3
B. m < 3
C. m > - 3
D. m < - 3
Tìm tất cả các giá trị thực của tham số m để đường thẳng y= - mx cắt đồ thị của hàm số y= x3- 3x2-m+ 2 tại ba điểm phân biệt A; B; C sao cho AB= BC.
A. m< 1
B. m> 2
C. m < 3
D. m> 4
+ Hoành độ giao điểm là nghiệm của phương trình
x3- 3x2-m+ 2= -mx hay ( x-1) ( x2-2x+ m-2) =0
Hay x=1; x2-2x+m-2=0
+ Đặt nghiệm x2= 1; từ giải thiết bài toán trở thành tìm m để phương trình có 3 nghiệm lập thành cấp số cộng. Khi đó phương trình : x2-2x+m-2 = 0 phải có 2 nghiệm phân biệt (vì theo hệ thức Viet ta có: x1+ x3= 2= 2x2 ).
Vậy khi đó ta cần ∆’ > 0( để phương trình có 2 nghiệm phân biệt )
∆’=1-(m-2)>0 ⇔ m < 3
Chọn C.
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị của tham số m để đường thẳng
y
(
m
-
1
)
x
cắt đồ thị hàm số
y
x
3
-
3
x
2
+
m
+
1
tại 3 điểm phân biệt A, B, C sao cho ABBC A.
m
∈
(
-
∞
;
0
]
∪
[
4
;
+
∞
)
B.
m...
Đọc tiếp
Tìm tất cả các giá trị của tham số m để đường thẳng y = ( m - 1 ) x cắt đồ thị hàm số y = x 3 - 3 x 2 + m + 1 tại 3 điểm phân biệt A, B, C sao cho AB=BC
A. m ∈ ( - ∞ ; 0 ] ∪ [ 4 ; + ∞ )
B. m ∈ ( - 5 4 ; + ∞ )
C. m ∈ ( - 2 ; + ∞ )
D. m ∈ ℝ
Đáp án C
Số giao điểm của đường thẳng y = ( m - 1 ) x và đồ thị hàm số y = x 3 - 3 x 2 + m + 1 là số nghiệm của PT x 3 - 3 x 2 + m + 1 = ( m - 1 ) x ⇔ x 3 - 3 x 2 + x + 1 - m x + m = 0 ⇔ ( x - 1 ) ( x 2 - 2 x - m - 1 ) = 0 để tồn tại ba giao điểm phân biệt thì 1 - 2 - m - 1 ≢ 0 ∆ ' = 1 + m + 1 > 0 ⇔ m ≢ - 2 m > - 2 khi đó tọa độ ba giao điểm là B ( 1 ; m - 1 ) , A ( x 1 ; y 1 ) , C ( x 2 ; y 2 ) hơn nữa x 1 + x 2 2 = 1 y 1 + y 2 2 = ( m - 1 ) x 1 + ( m - 1 ) x 2 2 = ( m - 1 ) ( x 1 + x 2 ) 2 = m - 1
⇒ B là trung điểm AC hay ta có AB=BC
Đúng 0
Bình luận (0)
Tìm m để đồ thị (C) của
y
x
3
−
3
x
2
+
4
và đường thẳng
y
m
x
+
m
cắt nhau tại 3 điểm phân biệt
A
−
1
;
0
,
B
,
C
sao cho
Δ
O
B
C
c...
Đọc tiếp
Tìm m để đồ thị (C) của y = x 3 − 3 x 2 + 4 và đường thẳng y = m x + m cắt nhau tại 3 điểm phân biệt A − 1 ; 0 , B , C sao cho Δ O B C có diện tích bằng 8.
A. m=4
B. m=3
C.m=1
D.m=2
Đáp án A
Xét PT
x 3 − 3 x 2 + 4 = m x + m ⇔ x + 1 x 2 − 4 x + 4 − m = 0 ;
ĐK để PT này có ba ngiệm là m > 0 và m ≠ 9
Khoảng các từ tới đường thẳng y = m x + m là: h = m m 2 + 1 = m m 2 + 1
Gọi tọa độ của
B x 1 ; y 1 , C x 2 ; y 2 ⇒ B C = x 2 − x 1 2 + y 2 − y 1 2 = x 2 − x 1 2 + m 2 x 2 − x 1 2
= m 2 + 1 x 2 − x 1 2 = m 2 + 1 x 2 + x 1 2 − 4 x 1 x 2 = 4 m m 2 + 1
⇒ S O B C = 1 2 h . B C = 1 2 m m 2 + 1 4 m m 2 + 1 =8 ⇒ m = 4
Đúng 0
Bình luận (0)
Với giá trị nào của m thì đồ thị hàm số
y
x
3
+
3
x
2
+
m
+
2
cắt trục hoành tại ba điểm phân biệt? Biết đồ thị hàm số
y
x
3
+
3
x
2
+
2
được cho như hình vẽ. A.
m
2
B. ...
Đọc tiếp
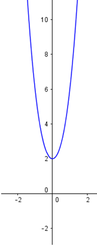
Với giá trị nào của m thì đồ thị hàm số y = x 3 + 3 x 2 + m + 2 cắt trục hoành tại ba điểm phân biệt? Biết đồ thị hàm số y = x 3 + 3 x 2 + 2 được cho như hình vẽ.
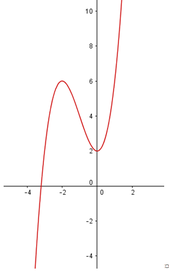
A. m > 2
B. m < 2
C. Không có giá trị nào của m thỏa mãn
D. m ≥ 2
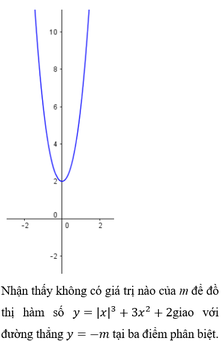
Với giá trị nào của m thì đồ thị hàm số
y
|
x
3
|
+
3
x
2
+
m
+
2
cắt trục hoành tại ba điểm phân biệt? Biết đồ thị hàm số
y
x...
Đọc tiếp
Với giá trị nào của m thì đồ thị hàm số y = | x 3 | + 3 x 2 + m + 2 cắt trục hoành tại ba điểm phân biệt? Biết đồ thị hàm số y = x 3 + 3 x 2 + 2 được cho như hình vẽ .
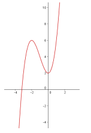
A. m > 2
B. m ≥ 2
C. m < 2
D. Không có giá trị nào của m thỏa mãn