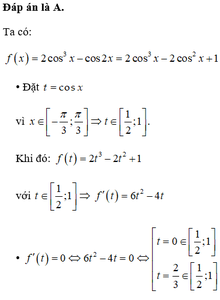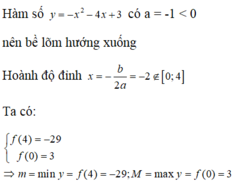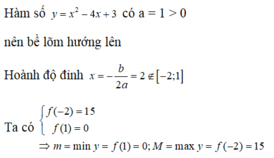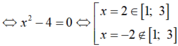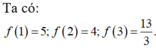tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x) = ( x +3 )( 5 - x ) với -3<= x <=5

Những câu hỏi liên quan
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số
f
(
x
)
2
c
o
s
3
x
-
c
o
s
2
x
trên đoạn D[
-
π
/
3
;
π
/
3
] A.
m
a
x
(
x
∈...
Đọc tiếp
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số f ( x ) = 2 c o s 3 x - c o s 2 x trên đoạn D=[ - π / 3 ; π / 3 ]
A. m a x ( x ∈ D ) f ( x ) = 1 ; m i n ( x ∈ D ) f ( x ) = 19 / 27
B. m a x ( x ∈ D ) f ( x ) = 3 / 4 ; m i n ( x ∈ D ) f ( x ) = - 3
C. m a x ( x ∈ D ) f ( x ) = 1 ; m i n ( x ∈ D ) f ( x ) = - 3
D. m a x ( x ∈ D ) f ( x ) = 3 / 4 ; m i n ( x ∈ D ) f ( x ) = 19 / 27
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau: f(x) = 1/sinx trên đoạn [ π /3; 5 π /6]
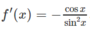
f′(x) < 0 nên và f’(x) > 0 trên ( π /2; 5 π /6] nên hàm số đạt cực tiểu tại x = π /2 và f CT = f( π /2) = 1
Mặt khác, f( π /3) = 2 3 , f(5 π /6) = 2
Vậy min f(x) = 1; max f(x) = 2
Đúng 0
Bình luận (0)
Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số y = f ( x ) = − x 2 − 4 x + 3 trên đoạn [0;4]
A. M = 4; m = 0
B. M = 29; m = 0
C. M = 3; m = -29
D. M = 4; m = 3
Cho hàm số f(x) có đạo hàm là hàm f(x). Đồ thị hàm số f(x) như hình vẽ bên. Biết rằng f(0) + f(1) - 2f(2) f(4) - f(3). Tìm giá trị nhỏ nhất m và giá trị lớn nhất M của f(x) trên đoạn [0;4]. A. m f(4), M f(2) B. m f(1), M f(2) C. m f(4), M f(1) D. m f(0), M f(2)
Đọc tiếp
Cho hàm số f(x) có đạo hàm là hàm f'(x). Đồ thị hàm số f'(x) như hình vẽ bên. Biết rằng f(0) + f(1) - 2f(2) = f(4) - f(3). Tìm giá trị nhỏ nhất m và giá trị lớn nhất M của f(x) trên đoạn [0;4].

A. m = f(4), M = f(2)
B. m = f(1), M = f(2)
C. m = f(4), M = f(1)
D. m = f(0), M = f(2)
Chọn A
Dựa vào đồ thị của hàm f'(x) ta có bảng biến thiên.
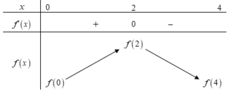
Vậy giá trị lớn nhất M = f(2)
Hàm số đồng biến trên khoảng (0;2) nên f(2) > f(1) => f(2) - f(1) > 0 .
Hàm số nghịch biến trên khoảng (2;4) nên f(2) > f(3) => f(2) - f(3) > 0.
Theo giả thuyết: f(0) + f(1) - 2f(2) = f(4) - f(3).
![]()
=> f(0) > f(4)
Vậy giá trị nhỏ nhất m = f(4)
Đúng 0
Bình luận (0)
Tìm giá trị lớn nhất và nhỏ nhất của hàm số \(f\left(x\right)=\sqrt{x+1}+\sqrt{3-x}\)
ĐKXĐ : \(-1\le x\le3\)
- ADbu nhi : \(\left(\sqrt{x+1}+\sqrt{3-x}\right)^2\le\left(1^2+1^2\right)\left(\left(\sqrt{x+1}\right)^2+\left(\sqrt{3-x}\right)^2\right)\)
\(=2\left(x+1+3-x\right)=2.4=8\)
\(\Rightarrow\sqrt{x+1}+\sqrt{3-x}\le\sqrt{8}=2\sqrt{2}\)
- Dấu " = " xảy ra \(\Leftrightarrow\dfrac{1}{\sqrt{x+1}}=\dfrac{1}{\sqrt{3-x}}\)
\(\Leftrightarrow x+1=3-x\)
\(\Leftrightarrow x=1\left(TM\right)\)
\(\Rightarrow Max_{f\left(x\right)}=2\sqrt{2}\) tại x = 1.
- Có : \(\sqrt{x+1}+\sqrt{3-x}\ge\sqrt{x+1+3-x}=\sqrt{4}=2\)
- Dấu " = " xảy ra <=> x = -1 ( TM )
\(\Rightarrow Min_{f\left(x\right)}=2\) tại x = - 1 .
Đúng 2
Bình luận (0)
Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số y = f(x) = x 2 − 4x + 3 trên đoạn [−2; 1].
A. M = 15; m = 1.
B. M = 15; m = 0.
C. M = 1; m = −2.
D. M = 0; m = −15.
Tích của giá trị nhỏ nhất và giá trị lớn nhất của hàm số
f
(
x
)
x
+
4
x
trên đoạn [1; 3] bằng. A. 20. B. 6. C. . D. .
Đọc tiếp
Tích của giá trị nhỏ nhất và giá trị lớn nhất của hàm số f ( x ) = x + 4 x trên đoạn [1; 3] bằng.
A. 20.
B. 6.
C. ![]() .
.
D. ![]() .
.
Tìm giá trị lớn nhất của hàm số :
C = -|x+4/7|+12/19
Tìm giá trị nhỏ nhất của hàm số :
D=|x-5/7|+2/3
F=|x-20|+|x-2015|
\(C=-\left|x+\frac{4}{7}\right|+\frac{12}{19}\)
Ta có: \(\left|x+\frac{4}{7}\right|\ge0\)nên \(-\left|x+\frac{4}{7}\right|\le0\)
\(\Rightarrow C=-\left|x+\frac{4}{7}\right|+\frac{12}{19}\le\frac{12}{19}\)
\(\Rightarrow C_{max}=\frac{12}{19}\)
(Dấu "="\(\Leftrightarrow x=\frac{-4}{7}\))
Đúng 0
Bình luận (0)
\(D=\left|x-\frac{5}{7}\right|+\frac{2}{3}\)
Vì \(\left|x-\frac{5}{7}\right|\ge0\)nên \(D=\left|x-\frac{5}{7}\right|+\frac{2}{3}\ge\frac{2}{3}\)
\(\Rightarrow D_{min}=\frac{2}{3}\)
(Dấu "="\(\Leftrightarrow x=\frac{5}{7}\))
Đúng 0
Bình luận (0)
\(F=\left|x-20\right|+\left|x-2015\right|\)
\(\Rightarrow F=\left|x-20\right|+\left|2015-x\right|\ge\left|\left(x-20\right)+\left(2015-x\right)\right|\)
\(=\left|2015-20\right|=\left|1995\right|=1995\)
\(\Rightarrow F_{min}=1995\)
(Dấu "="\(\Leftrightarrow x\le2015\))
Đúng 0
Bình luận (0)
Cho hàm số
y
f
(
x
)
x
-
m
2
x
+
4
với m là số thực. Tìm giá trị lớn nhất của m để hàm số f(x) có giá trị nhỏ nhất trên [0;1] bằng -1 A. m 2 B. m 0 C.
m
6
D. m 3
Đọc tiếp
Cho hàm số y = f ( x ) = x - m 2 x + 4 với m là số thực. Tìm giá trị lớn nhất của m để hàm số f(x) có giá trị nhỏ nhất trên [0;1] bằng -1
A. m = 2
B. m = 0
C. m 6
D. m = 3