Cho hai tia ox và oy vuông góc , trong góc xôy . vẽ 2 tia OA , OB sao cho aôx = BÔy = \(30^0\) . Vẽ tia OC sao cho Oy là tia phân giác của góc aôC .
Chứng minh :
a) Khi OA là phân giác của Bôx
b) OB vuông góc OC
Cho hai tia Õ và Oy vuông góc với nhau.Trong góc xÔy vẽ hai tia OA và OB sao cho AÔx=BÔy=30 độ.Vẽ tia OC sao cho Oy la tia phân giác của góc AOC. Chứng tỏ rằng:
a) Tia OA là tia phân giác của góc BÔx
b) OB vuông góc với OC
a: \(\widehat{BOA}=90^0-30^0-30^0=30^0\)
\(\Leftrightarrow\widehat{BOA}=\widehat{xOA}\)
hay OA là tia phân giác của góc BOx
b: \(\widehat{COy}=\widehat{AOy}=60^0\)
\(\Leftrightarrow\widehat{COB}=\widehat{COy}+\widehat{yOB}=60^0+30^0=90^0\)
hay OB\(\perp\)OC
Cho hai tia Ox, Oy vuông góc với nhau. Vẽ phía trong góc xOy, vẽ hai tia OA, OB sao cho góc xOA = yOB = 30○.
a) Chứng minh: tia OA là tia phân giác góc xOB.
b) Vẽ tia OC sao cho Oy là tia phân giác của góc AOC. Chứng minh: OB vuông góc với OC.
a,Do \(\widehat{yOB}\)<\(\widehat{yOx}\)và tia OB nằm trong góc \(\widehat{xOy}\)
\(\Rightarrow\)Tia OB nằm giữa hai tia Ox,Oy
\(\Rightarrow\)\(\Rightarrow\widehat{yOB}\)+\(\widehat{BOx}\)=\(\widehat{xOy}\)
\(\Rightarrow30^o+\widehat{BOx}\)\(=90^o\)
\(\Rightarrow\widehat{BOx}\)\(=60^o\)
Do \(\widehat{xOA}\)<\(\widehat{xOB}\)và hai tia OA,OB cùng nằm trong \(\widehat{xOy}\)
\(\Rightarrow\widehat{xOA}+\widehat{AOB}=\widehat{xOB}\)
\(\Rightarrow30^o+\widehat{AOB}=60^o\)
\(\Rightarrow\widehat{AOB}=30^o\)
Do \(\widehat{xOA}=\widehat{AOB}\)\(=\frac{\widehat{BOx}}{2}=\frac{60^o}{2}=30^o\)
\(\Rightarrow\)Tia OA là tia phân giác của \(\widehat{xOB}\)
b, mk chịu
Cho hai tia OX vuông góc OY, trong XOY ta vẽ hai tia OA, OB sao cho AOx=BOy=30 độ. Vẽ tia OC sao cho tia Oy là tia phân giác của AOC. Chứng minh rằng:
a ..Tia OA là tia phân giác BOx.
b.. OB vuông góc OC
Cho hai tia Ox và Oy vuông góc với nhau. Trong góc x O y ^ , ta vẽ hai tia Oa và Ob sao cho a O x ^ = b O y ^ = 30 ° . Vẽ tia Oc sao cho tia Oy là tia phân giác của a O c ^ . Chứng tỏ tia Oa là phân giác của b O x ^ và hai tia Ob, Oc vuông góc với nhau.
Cho hai tia Ox và Oy vuông góc với nhau. Trong góc x O y ^ , ta vẽ hai tia Oa và Ob sao cho a O x ^ = b O y ^ = 30°. Vẽ tia Oc sao cho tia Oy là tia phân giác của a O c ^ . Chứng tỏ tia Oa là phân giác của b O x ^ và hai tia Ob, Oc vuông góc với nhau
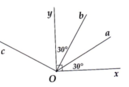
Ta có: a O b ^ = 30°= x O a ^ suy ra
Oa là phân giác của b O x ^ .
Lại có a O y ^ = 60°, Oy là phân
giác của a O c ^ nên:
y O c ^ = a O y ^ = 60°.
Khi. đó:
b O c ^ = b O y ^ + y O c ^ = 90°.
v
cho hai tia Ox và Oy vuông góc với nhau.Trong góc xOy vẽ hai tia OA và OB sao cho góc AOx=góc BOy=30 độ .Vẽ tia OC sao cho Oy là tia phân giác của góc AOC . Chứng tỏ rằng:
a, Tia OA là tia phân giác của góc BOx.
b, OB vuông góc với OC
a) Ta có: \(\widehat{xOA}+\widehat{AOB}+\widehat{yOB}=90^0\)
\(\Leftrightarrow\widehat{AOB}=90^0-30^0-30^0=30^0\)
Ta có: tia OA nằm giữa hai tia Ox và OB
mà \(\widehat{xOA}=\widehat{BOA}\left(=30^0\right)\)
nên OA là tia phân giác của \(\widehat{xOB}\)
Bài 4. Cho hai tia Ox Oy ; vuông góc với nhau. Trong góc xOy vẽ hai tia Oa; Ob sao cho aOx=bOy=30 . Vẽ tia Oc sao cho Oy là phân giác của aOc . Chứng tỏ rằng
a. tia Oa là tia phân giác của bOx .
b. Ob⊥Oc .
Giải:
a) Vì Ox và Oy vuông góc với nhau
\(\Rightarrow x\widehat{O}y=90^o\)
\(\Rightarrow x\widehat{O}a+a\widehat{O}b+b\widehat{O}y=x\widehat{O}y\)
\(30^o+a\widehat{O}b+30^o=90^o\)
\(a\widehat{O}b=90^o-30^o-30^o\)
\(a\widehat{O}b=30^o\)
\(\Rightarrow x\widehat{O}a+a\widehat{O}b=x\widehat{O}b\)
\(30^o+30^o=x\widehat{O}b\)
\(\Rightarrow x\widehat{O}b=60^o\)
Vì +) \(x\widehat{O}a+a\widehat{O}b=x\widehat{O}b\)
+) \(x\widehat{O}a=a\widehat{O}b=30^o\)
⇒Oa là tia p/g của \(x\widehat{O}b\)
Bài 5. Vẽ hai tia Ox vuông góc Oy. Trong 𝑥𝑂𝑦 ̂ , vẽ hai tia OA, OB sao cho 𝐴𝑂𝑥 ̂ = 𝐵𝑂𝑦 ̂. Vẽ tia OC sao cho Oy là tia phân giác 𝐴𝑂𝐶 ̂. a. Chứng minh : OA là tia phân giác 𝐵𝑂𝑥 ̂ b. OB vuông góc OC.
Bài 5. Vẽ hai tia Ox vuông góc Oy. Trong 𝑥𝑂𝑦 ̂ , vẽ hai tia OA, OB sao cho 𝐴𝑂𝑥 ̂ = 𝐵𝑂𝑦 ̂. Vẽ tia OC sao cho Oy là tia phân giác 𝐴𝑂𝐶 ̂. a. Chứng minh : OA là tia phân giác 𝐵𝑂𝑥 ̂ b. OB vuông góc OC.