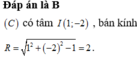Đường tròn 2x²+2y²-8x+4y-1=0 có tọa độ tâm là

Những câu hỏi liên quan
Trong không gian Oxyz cho mặt phẳng (P): 2x – 2y – z – 4 0 và mặt cầu (S):
x
2
+
y
2
+
z
2
-
2
x
-
4
y
-
6
z
-...
Đọc tiếp
Trong không gian Oxyz cho mặt phẳng (P): 2x – 2y – z – 4 = 0 và mặt cầu (S): x 2 + y 2 + z 2 - 2 x - 4 y - 6 z - 11 = 0 . Biết rằng mặt phẳng (P) cắt mặt cầu (S) theo một đường tròn (C). Tọa độ điểm H là tâm đường tròn (C) là:
A. H(3;0;2)
B. H(–1;4;4)
B. H(–1;4;4)
D. H(4;4; –1)
Đáp án A.
Phương pháp:
Mặt phẳng (P) cắt (S) theo một đường tròn (C) => Tâm H của (C) là hình chiếu của H trên (P).
Cách giải: Mặt cầu (S) có tâm I(1;2;3), bán kính R = 5
Mặt phẳng (P) cắt (S) theo một đường tròn (C) => Tâm H của (C) là hình chiếu của H trên (P)
Ta có n ( P ) → = ( 2 ; - 2 ; - 1 ) đường thẳng đi qua I và vuông góc với (P) có phương trình
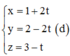
Khi đó ![]() . Thay vào phương trình mặt phẳng (P) ta có: 2(1+2t) – 2(2–2t) – (3–t) – 4 = 0 ó 9t – 9 = 0 ó t = 1 ó H(3;0;2)
. Thay vào phương trình mặt phẳng (P) ta có: 2(1+2t) – 2(2–2t) – (3–t) – 4 = 0 ó 9t – 9 = 0 ó t = 1 ó H(3;0;2)
Đúng 0
Bình luận (0)
Trong không gian Oxyz cho mặt phẳng (P): 2x-2y-z-40 và mặt cầu (S):
x
2
+
y
2
+
z
2
-
2
x
-
4
y
-
6
z
-
11
0
. Biết rằng m...
Đọc tiếp
Trong không gian Oxyz cho mặt phẳng (P): 2x-2y-z-4=0 và mặt cầu (S): x 2 + y 2 + z 2 - 2 x - 4 y - 6 z - 11 = 0 . Biết rằng mặt phẳng (P) cắt mặt cầu (S) theo một đường tròn (C). Tọa độ điểm H là tâm đường tròn (C) là:
A. H(3;0;2)
B. H(-1;4;4)
C. H(2;0;3)
D. H(4;4;-1)
Đáp án A.
Phương pháp:
Mặt phẳng (P) cắt (S) theo một đường tròn (C) => Tâm H của (C) là hình chiếu của H trên (P).
Cách giải: Mặt cầu (S) có tâm I(1;2;3) và bán kính R =5
Mặt phẳng (P) cắt (S) theo một đường tròn (C) => Tâm H của (C) là hình chiếu của H trên (P)
![]()
đường thẳng đi qua I và vuông góc với (P) có phương trình
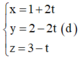
![]()
Thay vào phương trình mặt phẳng (P) ta có:
![]()
![]()
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, cho đường tròn
C
:
x
2
+
y
2
+
2
x
-
4
y
+
1
0
. Ảnh của đường tròn (C) qua phép vị tự tâm O tỷ sốk 2 có phương trình là A.
x
2
+
y
2
+
4
x
-
8
y...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho đường tròn C : x 2 + y 2 + 2 x - 4 y + 1 = 0 . Ảnh của đường tròn (C) qua phép vị tự tâm O tỷ số
k = 2 có phương trình là
A. x 2 + y 2 + 4 x - 8 y + 4 = 0
B. x 2 + y 2 - 4 x + 8 y + 4 = 0
C. x 2 + y 2 + 4 x - 8 y - 4 = 0
D. x 2 + y 2 + 4 x - 8 y + 2 = 0
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C):
x
2
+
y
2
+
2
x
-
4
y
+
1
0
. Ảnh của đường tròn (C) qua phép vị tự tâm O tỷ số k-2 có phương trình là A.
x
2
+
y
2
+
4
x
-
8...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C): x 2 + y 2 + 2 x - 4 y + 1 = 0 . Ảnh của đường tròn (C) qua phép vị tự tâm O tỷ số k=-2 có phương trình là
A. x 2 + y 2 + 4 x - 8 y + 4 = 0
B. x 2 + y 2 - 4 x + 8 y + 4 = 0
C. x 2 + y 2 + 4 x - 8 y + 4 = 0
D. x 2 + y 2 + 4 x - 8 y + 2 = 0
Trong không gian Oxyz, cho mặt cầu (S): x 2 + y 2 + z 2 - 2x + 4y + 2z - 19 = 0 và mặt phẳng (P): x - 2y + 2z - 12 = 0. Tìm tọa độ tâm và bán kính của đường tròn đó.
Gọi d là đường thẳng qua I và vuông góc với (P). Phương trình của d là
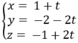
Tâm của (C) là điểm H = d ∩ (P). Để tìm H ta thay phương trình của d vào phương trình của (P).
Ta có: 1 + t - 2(-2 - 2t) + 2(-1 + 2t) - 12 = 0
Suy ra t = 1, do đó H = (2; -4; 1).
Bán kính của (C) bằng
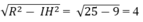
Đúng 0
Bình luận (0)
Phương trình nào trong các phương trình sau đây là phương trình đường tròn? Tìm tọa độ tâm và bán kính của đường tròn đó.
a) \({x^2} + {y^2} - 6x - 8y + 21 = 0\)
b) \({x^2} + {y^2} - 2x + 4y + 2 = 0\)
c) \({x^2} + {y^2} - 3x + 2y + 7 = 0\)
d) \(2{x^2} + 2{y^2} + x + y - 1
a) Phương trình đã cho có dạng \({x^2} + {y^2} - 2ax - 2by + c = 0\) với \(a = 3,b = 4,c = 21\)
Ta có \({a^2} + {b^2} - c = 9 + 16 - 21 = 4 > 0\). Vậy đây là phương trình đường tròn có tâm là \(I(3;4)\) và có bán kính \(R = \sqrt 4 = 2\)
b) Phương trình đã cho có dạng \({x^2} + {y^2} - 2ax - 2by + c = 0\) với \(a = 1,b = - 2,c = 2\)
Ta có \({a^2} + {b^2} - c = 1 + 4 - 2 = 3 > 0\). Vậy đây là phương trình đường tròn có tâm là \(I(1; - 2)\) và có bán kính \(R = \sqrt 3 \)
c) Phương trình đã cho có dạng \({x^2} + {y^2} - 2ax - 2by + c = 0\) với \(a = \frac{3}{2},b = - 1,c = 7\)
Ta có \({a^2} + {b^2} - c = \frac{9}{4} + 1 - 7 = - \frac{{15}}{4} < 0\). Vậy đây không là phương trình đường tròn.
d) Phương trình không có dạng \({x^2} + {y^2} - 2ax - 2by + c = 0\) nên phương trình đã cho không là phương trình đường tròn.
Đúng 0
Bình luận (0)
Tìm tọa độ tâm I và bán kính R của đường tròn (C): x 2 + y 2 - 2 x + 4 y + 1 = 0
A. I (-1;2) ; R = 4
B. I (1;-2) ; R = 2
C. I (-1;2) ; R = 5
D. I (1;-2) ; R = 4
Tìm tọa độ tâm I và bán kính R của đường tròn (C):
x
2
+
y
2
-
2
x
+
4
y
+
1
0
A. I(-1;2); R4 B. I(1;-2); R2 C.
I
-
1
;
2
;
R
5
B. I(1;-2); R2
Đọc tiếp
Tìm tọa độ tâm I và bán kính R của đường tròn (C): x 2 + y 2 - 2 x + 4 y + 1 = 0
A. I(-1;2); R=4
B. I(1;-2); R=2
C. I - 1 ; 2 ; R = 5
B. I(1;-2); R=2
Trong mặt phẳng với hệ tọa độ
Ox
y
cho đường tròn
C
:
x
2
+
y
2
−
2
x
−
4
y
+
4
0
và đường tròn
C
:
x
2
+
y
2
+
6
x...
Đọc tiếp
Trong mặt phẳng với hệ tọa độ Ox y cho đường tròn C : x 2 + y 2 − 2 x − 4 y + 4 = 0 và đường tròn C ' : x 2 + y 2 + 6 x + 4 y + 4 = 0. Tìm tâm vị tự của hai đường tròn?
A. I 0 ; 1 v à J 3 ; 4
B. I − 1 ; − 2 v à J 3 ; 2
C. I 1 ; 2 v à J − 3 ; − 2
D. I 1 ; 0 v à J 4 ; 3
Đáp án A
Đường tròn C có tâm K 1 ; 2 , bán kính R = 1 + 4 − 4 = 1 .
Đường tròn C ' có tâm K ' − 3 ; − 2 , bán kính R ' = 9 + 4 − 4 = 3.
Giả sử V 1 ; k C = C '
khi đó k = R ' R ⇒ k = 3 ⇔ k = ± 3
Với k = 3 ⇒ I K ' → = 3 I K → ⇒ − 3 − x 1 = 3 1 − x 1 − 2 − y 1 = 3 2 − y 1 ⇒ I 3 ; 4
Với k = − 3 ⇒ I K ' → = − 3 I K → ⇒ − 3 − x 1 = − 3 1 − x 1 − 2 − y 1 = − 3 2 − y 1 ⇒ I 0 ; 1
Đúng 0
Bình luận (0)