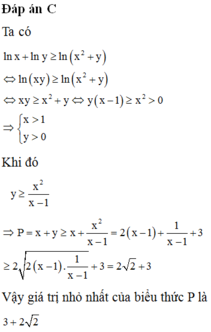Cho 2 số dương x,y thỏa

Những câu hỏi liên quan
a)Tìm các số nguyên dương x, y thỏa mãn x+3 chia hết cho y, y+3 chia hết cho x
b)Tìm các số nguyên dương x, y thỏa mãn xy+x+y+2 chia hết cho cả x và y.
Bài 8. Cho số nguyên dương n. Tồn tại hay không số nguyên dương d thỏa mãn: d là ước của 3n^2 và n^2 +d là số chính phương. Bài 9. Chứng minh rằng không tồn tại hai số nguyên dương x, y thỏa mãn x^2 +y+1 và y^2 +4x+3 đều là số chính phương.
Ai đó giúp mình đi mòaa🤤🤤🤤
Bài 1:Cho x, y là các số nguyên dương thỏa mãn x+y= 3.\(\sqrt{xy}\).Tinh x/ y
Bài 2: Tìm các số nguyên dương x, y thỏa mãn (1/x)+(1/y)=1/2
Tu de bai suy ra 2y+2x=xy<=>...<=>y(2-x)= -2x<=>y=2x/(x-2)<=>y=(2x-4+4)/(x-2)<=>y=2+4/(x-2)
vi x la so nguyen Dưỡng nen x-2 la so nguyen duong va la ước cua 4 => x-2 =1 hoặc x-2= 4 => x=3 hoac x=6
Voi x=3 => y= 6
voi x=6=> y=3
vay cac cap so nguyen duong (x;y) can tim la (3;6); (6;3)
Đúng 0
Bình luận (0)
.....
Sau khi chi ra x-2 la uoc nguyen duong cua 4
Co 3 Truong hop
x-2 =1; x-2=2;x-2=4
Tu do tinh duoc x=3;x=4;x=6. Suy ra cac gia tri tuong ung cua y
co 3 cap so nguyen duong x, y can Tim:(3;6);(4 ;4);(6;3)
Đúng 0
Bình luận (0)
Cho x, y là các số thực dương thỏa mãn lnx + lny ≥ ln(x2+y) là các số thực dương thỏa mãn P x + y A. P 6 B. P
2
+
3
2
C. P
3
+
2
2
D. P
17
+
3
Đọc tiếp
Cho x, y là các số thực dương thỏa mãn lnx + lny ≥ ln(x2+y) là các số thực dương thỏa mãn P = x + y
A. P = 6
B. P = 2 + 3 2
C. P = 3 + 2 2
D. P = 17 + 3
Đáp án C
Ta có
![]()

Khi đó

![]()
Vậy giá trị nhỏ nhất của biểu thức P là 3 + 2 2
Đúng 0
Bình luận (0)
Cho x, y là các số thực dương thỏa mãn
ln
x
+
ln
y
≥
ln
(
x
2
+
y
)
là các số thực dương thỏa mãn
P
x
+
y
Đọc tiếp
Cho x, y là các số thực dương thỏa mãn ln x + ln y ≥ ln ( x 2 + y ) là các số thực dương thỏa mãn P = x + y
![]()
![]()
![]()
![]()
Cho hai số dương x, y thỏa mãn: x + y = 2
CMR: x2y2(x2 + y2) ≤ 2
Với x, y là hai số dương, dễ dàng chứng minh x + y 2,
do x + y = 2 => 0 < xy ≤ 1 (1)
Ta lại có: 2xy( x2 + y2) ≤
=> 0 < 2xy(x2 + y2) ≤ (x+y)4/4 = 4
=> 0 < xy( x2 + y2) ≤ 2 (2)
Nhân (1) với (2) theo vế ta có: x2y2 ( x2 + y2) ≤ 2 (đpcm)
Dấu “=” xảy ra khi x = y = 1
Đúng 2
Bình luận (0)
Cho các số nguyên dương x, y, z thỏa mãn \(x^2+y^2=z^2\). Chứng minh rằng:
\(x+3z-y\) là hợp số.
refer
https://olm.vn/hoi-dap/detail/1303479279140.html
Đúng 2
Bình luận (0)
Cho các số nguyên dương x, y thỏa mãn \(x^2+y^2+2xy-2x+2y\) là một số chính phương. CM x=y
Cho 2 số dương x,y thỏa mãn x^3+y^3=xy. CM: x^2+y^2<1
Cho x,y là các số dương thỏa 18/x +2/y = 1. Tìm GTNN của A = x + y
\(1=2\left(\dfrac{9}{x}+\dfrac{1}{y}\right)\ge2.\dfrac{\left(3+1\right)^2}{x+y}=\dfrac{32}{x+y}\)
\(\Rightarrow x+y\ge32\)
\(A_{min}=32\) khi \(\left(x;y\right)=\left(24;8\right)\)
Đúng 2
Bình luận (0)