MN ơi giúp mình bài này cái

Giải hộ mình bài này cái MN ơi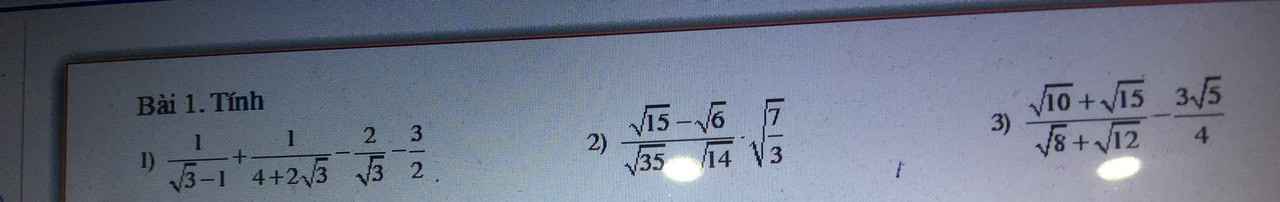
1) Ta có: \(\dfrac{1}{\sqrt{3}-1}+\dfrac{1}{4+2\sqrt{3}}-\dfrac{2}{\sqrt{3}}-\dfrac{3}{2}\)
\(=\dfrac{\sqrt{3}+1}{2}+\dfrac{2-\sqrt{3}}{2}-\dfrac{2\sqrt{3}}{3}-\dfrac{3}{2}\)
\(=\dfrac{\sqrt{3}+1+2-\sqrt{3}-3}{2}-\dfrac{2\sqrt{3}}{3}\)
\(=-\dfrac{2\sqrt{3}}{3}\)
3) Ta có: \(\dfrac{\sqrt{10}+\sqrt{15}}{\sqrt{8}+\sqrt{12}}-\dfrac{3\sqrt{5}}{4}\)
\(=\dfrac{\sqrt{5}\left(\sqrt{2}+\sqrt{3}\right)}{2\left(\sqrt{2}+\sqrt{3}\right)}-\dfrac{3\sqrt{5}}{4}\)
\(=\dfrac{2\sqrt{5}-3\sqrt{5}}{4}\)
\(=\dfrac{-\sqrt{5}}{4}\)
mn ơi cho mình hỏi với ạ, cái bài này làm kiểu gì vậy, mình không có biết á, mn ai biết giúp mình nha!
Đọc tiếp
Chào bạn, hiện tại câu hỏi của bạn chưa hiển thị trên diễn đàn. Có thể file bạn tải lên bị lỗi nên không hiển thị được. Bạn nên gõ trực tiếp đề bài lên Olm để tránh lỗi này và nhận được sự hỗ trợ nhanh hơn từ cộng đồng nhé!
@Phạm Lê Minh Vương (2) mình vẫn đọc đc mà, chắc lỗi á bạn
mn ơi, mn có thể giúp mình cái này đc ko, hiện tại ở trên lớp nhóm mk đang làm bài thuyết trình về truyện "Vua Chích Chòe", thì mình đang cần nhiều ảnh liên quan đến bài, càng nhiều ảnh càng tốt, mong mọi người giúp đỡ mk ạ
Mn ơi giúp mình 4 cái này đi ạ 🥺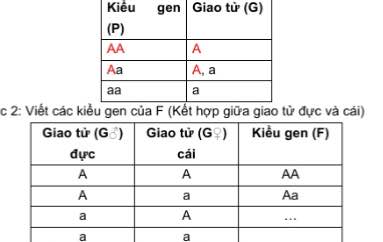

mn ơi giúp mình vẽ 3 cái hình chiếu của cái hình này với ạ :((((
Xin lũi vẽ bằng máy nên hơi xấu với độ Cm ko chuẩn ( muốn căn cho bằng nhau r mà ko đc)
Giúp giúp mình bài này với mn ơi

\(f'\left(x\right)=x^2+2x\)
a.
\(f'\left(-3\right)=3\) ; \(f\left(-3\right)=-2\)
Phương trình tiếp tuyến:
\(y=3\left(x+3\right)-2\Leftrightarrow y=3x+7\)
b.
Gọi \(x_0\) là hoành độ tiếp điểm, do hệ số góc tiếp tuyến bằng 3
\(\Rightarrow f'\left(x_0\right)=3\Rightarrow x_0^2+2x_0=3\Rightarrow x_0^2+2x_0-3=0\)
\(\Rightarrow\left[{}\begin{matrix}x_0=1\Rightarrow y_0=-\dfrac{2}{3}\\x_0=-3\Rightarrow y_0=-2\end{matrix}\right.\)
Có 2 tiếp tuyến thỏa mãn:
\(\left[{}\begin{matrix}y=3\left(x-1\right)-\dfrac{2}{3}=3x-\dfrac{11}{3}\\y=3\left(x+3\right)-2=3x+7\end{matrix}\right.\)
c. Tiếp tuyến song song (d) nên có hệ số góc bằng 8
Gọi \(x_0\) là hoành độ tiếp điểm \(\Rightarrow x_0^2+2x_0=8\)
\(\Rightarrow\left[{}\begin{matrix}x_0=2\Rightarrow y_0=\dfrac{14}{3}\\x_0=-4\Rightarrow y_0=-\dfrac{22}{3}\end{matrix}\right.\)
Có 2 tiếp tuyến thỏa mãn:
\(\left[{}\begin{matrix}y=8\left(x-2\right)+\dfrac{14}{3}=...\\y=8\left(x+4\right)-\dfrac{22}{3}=...\end{matrix}\right.\)
Giúp mình bài này vs MN ơi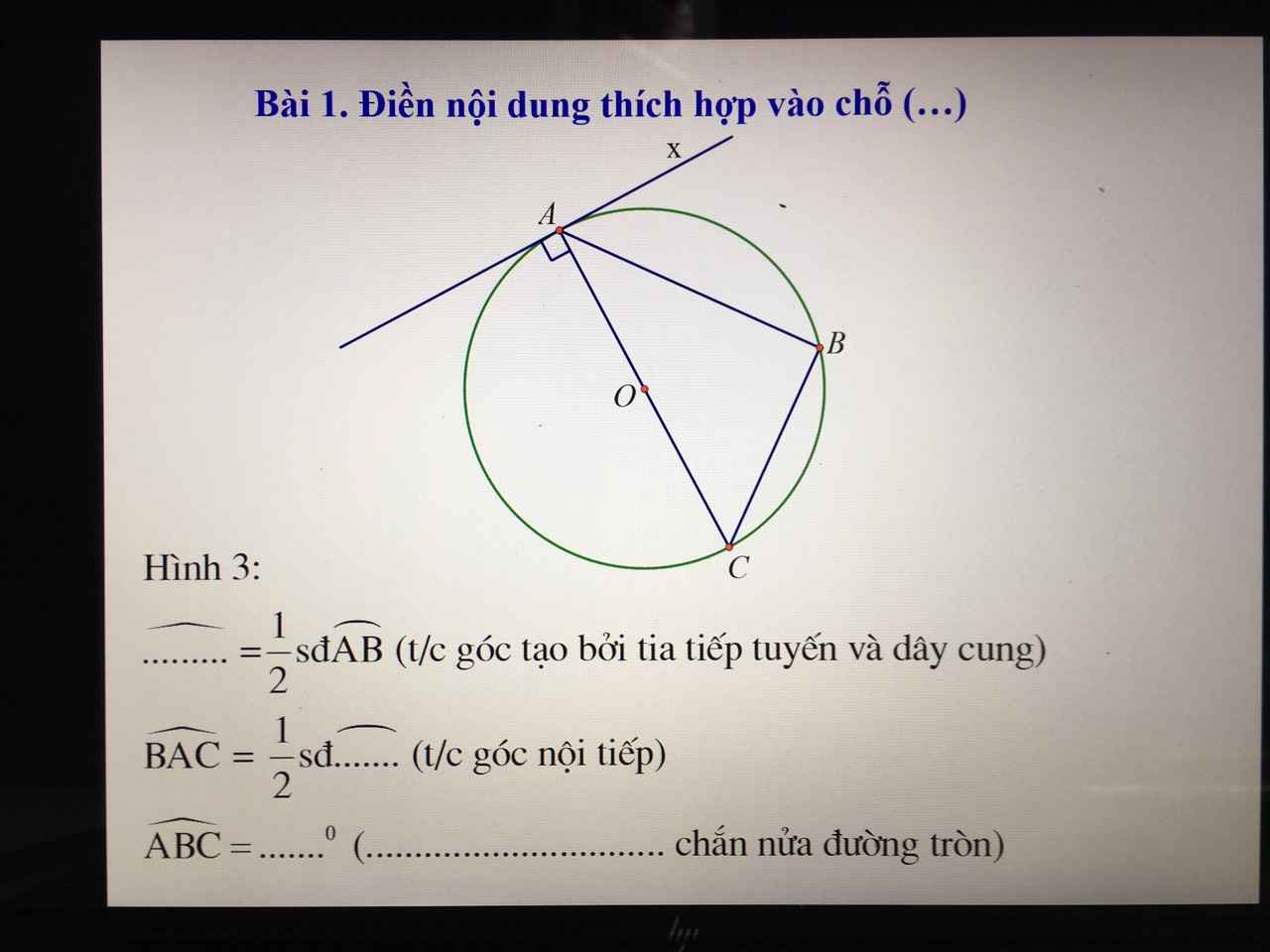
\(\widehat{BAx}=\dfrac{1}{2}sđ\stackrel\frown{AB}\)
\(\widehat{BAC}=\dfrac{1}{2}sđ\stackrel\frown{BC}\)
\(\widehat{ABC}=90^0\) (góc nội tiếp chắn nửa đường tròn)
Giúp mình bài này với mn ơi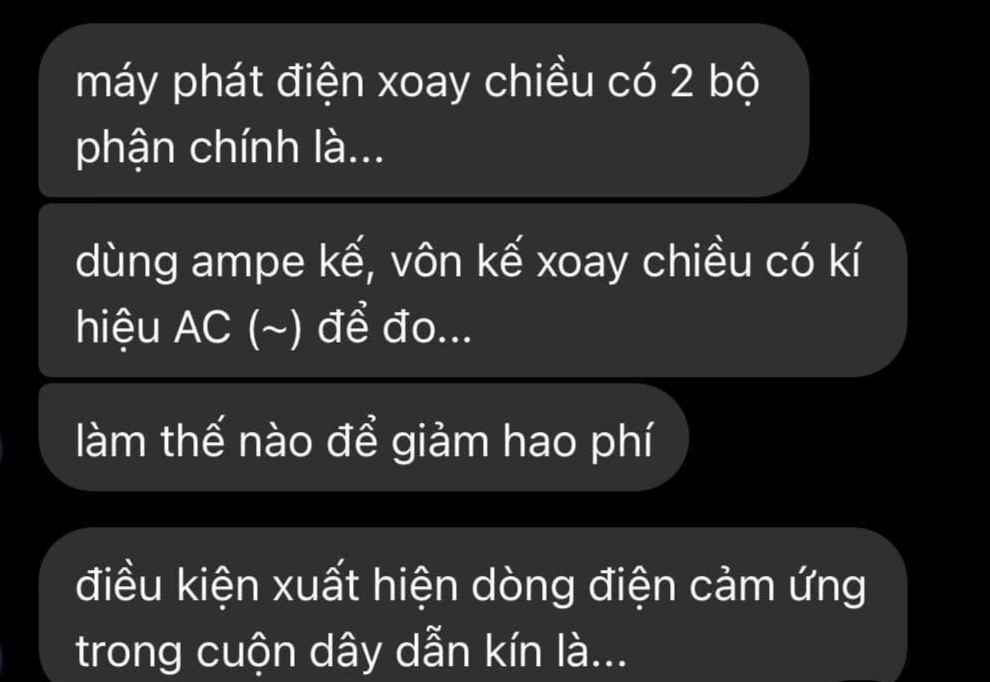
Giúp mình mấy bài này mn ơi

Bài 30:
Áp dụng BĐT Cauchy-Schwarz:
$\text{VT}=\frac{a^2}{ab+ac-a^2}+\frac{b^2}{ab+bc-b^2}+\frac{c^2}{cb+ca-c^2}\geq \frac{(a+b+c)^2}{2(ab+bc+ac)-(a^2+b^2+c^2)}$
Mà: $ab+bc+ac\leq a^2+b^2+c^2$ và $ab+bc+ac\leq \frac{(a+b+c)^2}{3}$ (theo BĐT AM-GM)
$\Rightarrow \text{VT}\geq \frac{(a+b+c)^2}{\frac{(a+b+c)^2}{3}}=3$
Ta có đpcm.
Dấu "=" xảy ra khi $a=b=c$
Cách 2 bài 30:
Đặt $b+c-a=x; a+c-b=y; b+a-c=z$ thì $x,y,z>0$ và $c=\frac{x+y}{2}; a=\frac{y+z}{2}; b=\frac{x+z}{2}$
Bài toán trở thành:
Cho $x,y,z>0$. CMR:
$\frac{y+z}{x}+\frac{x+z}{y}+\frac{x+y}{z}\geq 6$
-------------------------------
Thật vậy, áp dụng BĐT AM-GM thì:
$\text{VT}=(\frac{y}{x}+\frac{z}{y}+\frac{x}{z})+(\frac{z}{x}+\frac{x}{y}+\frac{y}{z})$
$\geq 3\sqrt[3]{\frac{yzx}{xyz}}+3\sqrt[3]{\frac{zxy}{xyz}}=6$ (đpcm)
Dấu "=" xảy ra khi $x=y=z$ hay $a=b=c$