bạn nào giúp mình với . Hãy chứng tỏ a//b bằng nhiều cách
Cho f(x)=ax^2+bc+c với a,b,c là các số hữu tỉ.
Chứng tỏ rằng:f(-2).f(3) nhỏ hơn hoặc bằng 0.biết rằng 13a+b+2c=0
Bạn nào biết cách giải thì giúp mình với nha! ( cách giải chi tiết)
Hãy chứng tỏ bốn chia ba bằng hai
Giúp mình với , trí nhớ mình kém nên quên hết rồi !
Ai trả lời đầu tiên giúp mình thì mình cảm ơn rất nhiều và sẽ kết bạn với người đó !!
Hãy chứng tỏ bốn chia ba bằng hai
4:3=tứ:tam=tám:tư(nói lái)=8:4=2!
^_^
bốn chia ba là tứ chia tam tứ chia tam là tám chia tư bằng 2
k mk nhé
Cho x,y thuộc Z. Hãy chứng tỏ rằng :
a,Nếu x - y > 0 thì x > y
b, Nếu x > y thì X - y > 0
Hãy giúp mình với. Mình cảm ơn các bạn nhiều
Cho hình dưới đây. Hãy chứng tỏ a // b bằng nhiều cách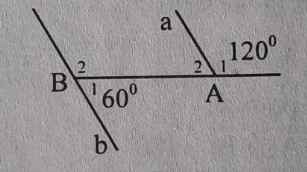
C1: Ta có: A2 = 180o - 120o = 60o
Ta thấy: B1 = A2 = 60o
=> a//b (so le trong)
C2: Ta có: A2 = 60o như cách 1.
Ta có: B2 = 180o - 60o = 120o
Ta thấy: B2 + A2 = 120o + 60o = 180o
=> a//b (2 góc trong cùng phía)
C3: ta có: B2 = 120o như cách 2.
Ta thấy: B2 = A2 = 120o
=> a//b (đồng vị)
\(\widehat{A_2}=180^0-120^0=60^0\)
Ta có: \(\widehat{A_2}=\widehat{B_1}\)
mà hai góc này là hai góc ở vị trí so le trong
nên a//b
Bài 4: Hãy chứng tỏ a // b bằng nhiều cách.
a//b
\(\widehat{B2}=\widehat{A1}\) (đồng vị)
\(\widehat{B1}=\widehat{A2}\) (so le trong)
1. Cho góc AOB , vẽ góc BOC và AOD là 2 góc kề bù với góc AOB . Hãy chứng tỏ góc BOC VÀ góc AOD là 2 góc đối đình
2, Hai đường thẳng EF và MN cắt nhau tại O tạo thành 4 góc ( ko kể góc bẹt ) biết tổng của 3 góc trong số đó 4 góc = 250độ 46 phút .
tính số đo của 4 góc ( bằng 2 cách )
Mình cần gấp lắm ạ . Bạn nào làm đúng và nhanh nhất mình sẽ tick cho ạ
Các bạn giúp mình vs ạ . Cảm ơn nhiều <3 ( vẽ hình giải chi tiết giúp mình vs ạ )
1. Do góc BOC kề bù với góc AOB
=> Tia OA và tia OC đối nhau
Do góc AOD và góc AOB kề bù
=> tia OD và tia OB đối nhau
=> góc BOC và góc AOD là 2 góc đối đỉnh
Gọi OM, ON là 2 tia phân giác góc AOD và góc BOC
=> góc AOM = 1/2 góc AOD = 1/2 (180* - 135*) = 45*/2
mà góc AON = góc AOB + góc BON
=> góc AON = 135* + 45*/2
=> góc AOM + góc AON = 135* + 45*/2 + 45*/2 = 180*
=> góc MON = 180*
=> OM , ON là 2 tia đối nhau
2. Gọi 4 góc cần tìm là .O1,O2,O3O4
Giả sử :O1+O2+O3=250°46'
=> O4=360°-250°46'=109°14'
=>O2=O4= 109°14' (đối đỉnh )
O1=O3= \(\frac{250°46'-109°14'}{2}=70°46'\)
cho tam giác abc có b=c=40. Gọi ax là tia phân giác của góc ngoài ở đỉnh a. Hãy chứng tỏ rằng ax song song bc ( Các bạn giúp mình cách làm và vẽ hình giúp mình lun nha mình cảm ơn nhìu )
Cho hình thang ABCD (AB // CD)
a) tính tổng A + D, suy ra trong hai góc A, D có nhiều nhất một góc tù.
b) chứng minh trong 2 góc B, C có nhiều nhất một góc tù.
[Mình biết cách làm nhưng mình không biết cách trình bày bạn nào giúp mình với!!!]
Cho A = 7 + 72 + 73 + ... + 778. Chứng tỏ rằng A chia hết cho 8
Cho A = 1050 + 68. Chứng tỏ rằng A chia hết cho 121
Cho A = 3 + 32 + 33 + ... + 3155. Chứng tỏ rằng A chia hết cho 121
Mấy bạn hiện đang là CTV hoặc các bạn biết cách làm thì giúp mình với. Cảm ơn các bạn nhiều.
1.
\(A=7+7^2+7^3+...+7^{78}\)
\(=\left(7+7^2\right)+\left(7^3+7^4\right)+...+\left(7^{77}+7^{78}\right)\)
\(=7\left(1+7\right)+7^3\left(1+7\right)+...+7^{77}\left(1+7\right)\)
\(=7\cdot8+7^3\cdot8+...+7^{77}\cdot8\)
\(=\left(7+7^3+...+7^{77}\right)\cdot8\) chia hết cho 8
Vậy A chia hết cho 8 (đpcm)
\(A=3+3^2+3^3+...+3^{155}\)
\(=\left(3+3^2+3^3+3^4+3^5\right)+...+\left(3^{151}+3^{152}+3^{153}+3^{154}+3^{155}\right)\)
\(=3\left(1+3+3^2+3^3+3^4\right)+...+3^{151}\left(1+3+3^2+3^3+3^4\right)\)
\(=\left(3+...+3^{151}\right)\cdot121\) chia hết cho 121
Vậy A chia hết cho 121 (đpcm)