CHo tam giác ABC vg tại A , đcao AH . Tính BH và CH biết AC = 16 cm và AB/AC = 3/4

Những câu hỏi liên quan
CHo tam giác ABC vg tại A , đcao AH . tính CH biết AB = 25 cm , AC = 5 căn 3 .
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=25^2+75=700\)
hay \(BC=10\sqrt{7}\left(cm\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AC^2=CH\cdot BC\)
\(\Leftrightarrow CH=\dfrac{75}{10\sqrt{7}}\)
hay \(CH=\dfrac{15\sqrt{7}}{14}\left(cm\right)\)
Đúng 2
Bình luận (0)
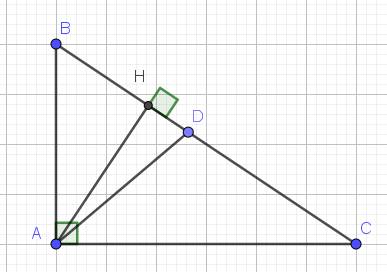
Cho tam giác ABC vuông tại A (AC > AB ) , đường cao AH . Biết BC= 5 cm , BH= 0.125 cm , M là trung điểm BC , đường trung trực BC cắt AC tại D.
a) Tính AB , AH .
b) Tính tỉ số diện tích của tam giác DMC và tam giác ABC .
tao chịu mày thế thì mày hỏi làm cái đéo gì hả ôn con
Đúng 0
Bình luận (0)
Bài 1:Cho tam giác nhọn ABC Kẻ AH vuông góc với BC(H thuộc BC), AB13 cm. AH12 cm. HC16 cm. Tính độ dài đoạn thẳng AC,BCBài 2: Cho tam giác ABC vuông tại A. Một đường thẳng cắt cạnh AB,AC ở D và E.Chứng minh CD2-CB2ED2-EB2Bài 3: Cho tam giác ABC vuông tại A có AB:AC8:15 và BC51 cma/ Tính độ dài AB,ACb/ Tính diện tích tam giác ABC4/Cho tam giác ABC cân tại A vẽ BC,CE lần lượt vuông góc với AC và AB. Gọi I là giao điểm của BD và CEa/ Chứng minh rằng...
Đọc tiếp
Bài 1:Cho tam giác nhọn ABC Kẻ AH vuông góc với BC(H thuộc BC), AB=13 cm. AH=12 cm. HC=16 cm. Tính độ dài đoạn thẳng AC,BC
Bài 2: Cho tam giác ABC vuông tại A. Một đường thẳng cắt cạnh AB,AC ở D và E.Chứng minh CD2-CB2=ED2-EB2
Bài 3: Cho tam giác ABC vuông tại A có AB:AC=8:15 và BC=51 cm
a/ Tính độ dài AB,AC
b/ Tính diện tích tam giác ABC
4/Cho tam giác ABC cân tại A vẽ BC,CE lần lượt vuông góc với AC và AB. Gọi I là giao điểm của BD và CE
a/ Chứng minh rằng tam giác AEI=tam giác ADI
b/ Gọi M là trung điểm BC. Chứng minh 3 điểm A,I,M thẳng hàng.
AI KO LÀM THÌ ĐỪNG CMT DÙM CÁI!
Bai 1:
Ap dung dinh li Py-ta-go vao tam giac AHB ta co:
AH^2+BH^2=AB^2
=>12^2+BH^2=13^2
=>HB=13^2-12^2=25
Tuong tu voi tam giac AHC
=>AC=20
=>BC=25+16=41
Đúng 0
Bình luận (0)
CHo tam giác ABC vg tại A , đcao AH . Tính BC nếu biết CH=3cm , AB = 3 căn 4 cm
CHo tam giác ABC vg tại A , đcao AH . Tính BC nếu biết CH=3cm , AB = 3✓4 cm
( Vẽ hình hộ )
Cho tam giác ABC cân tại A có đường cao AH.
a, Chứng minh tam giác ABH = tam giác ACH và AH là tia phân giác của góc BAC
b, Cho BH = 8cm, AB = 10cm. Tính AH
c, Gọi E là trung điểm của AC và G là giao điểm của BE và AH. Tính HG
d, Vẽ Hx song song với AC, Hx cắt AB tại F. Chứng minh C, G, F thẳng hàng
b, Cho BH = 8cm, AH = 10cm. Tính AH này là sao , biết AH mà còn bắt tính AH
Cho tam giác ABC vông tại A . Tính cạnh BC nếu biết :
3)AB+AC=17 cm và AB - AC = 7cm
4)AB+AC=14cm và AB-AC=2 cm
5)AB+AC=49 cm và AB - AC = 7 cm
3: \(\Leftrightarrow\left\{{}\begin{matrix}2AB=24\\AB-AC=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=12\\AC=5\end{matrix}\right.\)
=>BC=13
4: \(\Leftrightarrow\left\{{}\begin{matrix}2AB=16\\AB-AC=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=8\\AC=6\end{matrix}\right.\)
=>BC=10
5: \(\Leftrightarrow\left\{{}\begin{matrix}2AB=56\\AB-AC=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=28\\AC=21\end{matrix}\right.\)
=>BC=35
Đúng 1
Bình luận (0)
Lời giải:
3.
$AB=(17+7):2=12$ (cm)
$AC=(17-7):2=5$ (cm)
Áp dụng định lý Pitago: $BC=\sqrt{AB^2+AC^2}=\sqrt{12^2+5^2}=13$ (cm)
Các câu sau làm tương tự.
Đúng 1
Bình luận (0)
cho tam giác ABC vuông tại A biết AB = 3 , AC = 4 và đuòngw cao AH .
a, Tìm các cặp tam giác đồng dạng .
b, Tính AH , BC .
a. Có ba cặp tam giác đồng dạng:
▲ABC đồng dạng ▲HBA
▲ABC đồng dạng ▲HAC
▲HAC đồng dạng ▲HBA
b. Áp dụng định lý Pitago ta c/m được BC=5cm.
Ta có: SABC=\(\dfrac{1}{2}\)AB.AC=\(\dfrac{1}{2}\)AH.BC
=>AB.AC=AH.BC
=>AH=\(\dfrac{AB.AC}{BC}=\dfrac{3.4}{5}=\dfrac{12}{5}=2.4cm\)
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A và AB =12cm, AC =16cm .Đường phân giác góc A cắt BC tại D
a) Tính BC ,BD vad CD ĐS: BC =20cm , BD≈8,6cm ,DC≈11,4 cm
b) Vẽ đường cao AH .Tính AH ,HD và AD ĐS: AH ≈9.6 cm , HD ≈1,4cm , AD ≈9,7 cm
Lời giải:
a. Áp dụng định lý Pitago:
$BC=\sqrt{AB^2+AC^2}=\sqrt{12^2+16^2}=20$ (cm)
Áp dụng tính chất đường phân giác:
$\frac{BD}{DC}=\frac{AB}{AC}=\frac{12}{16}=\frac{3}{4}$
Mà: $BD+DC=BC=20$ nên:
$BD=20:(3+4).3=\frac{60}{7}$ (cm)
$CD= 20:(3+4).4=\frac{80}{7}$ (cm)
b.
$AH=2S_{ABC}:BC=\frac{AB.AC}{BC}=\frac{12.16}{20}=9,6$ (cm)
$BH=\sqrt{AB^2-AH^2}=\sqrt{12^2-9,6^2}=7,2$ (cm)
$HD = BD-BH = \frac{60}{7}-7,2=\frac{48}{35}$ (cm)
$AD = \sqrt{AH^2+HD^2}=\sqrt{9,6^2+(\frac{48}{35})^2}=\frac{48\sqrt{2}}{7}$ (cm)
Đúng 2
Bình luận (0)
a: Ta có: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=12^2+16^2=20^2\)
=>\(BC=20\left(cm\right)\)
Xét ΔABC có AD là phân giác
nên \(\dfrac{BD}{AB}=\dfrac{CD}{AC}\)
=>\(\dfrac{BD}{12}=\dfrac{CD}{16}\)
=>\(\dfrac{BD}{3}=\dfrac{CD}{4}\)
mà BD+CD=BC=20
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{3}=\dfrac{CD}{4}=\dfrac{BD+CD}{3+4}=\dfrac{20}{7}\)
=>\(BD=\dfrac{20}{7}\cdot3=\dfrac{60}{7}\left(cm\right);CD=\dfrac{20}{7}\cdot4=\dfrac{80}{7}\left(cm\right)\)
b: Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot20=12\cdot16=192\)
=>\(AH=\dfrac{192}{20}=9,6\left(cm\right)\)
Ta có: ΔAHB vuông tại H
=>\(HB^2+AH^2=AB^2\)
=>\(HB^2=12^2-9,6^2=51,84\)
=>\(HB=\sqrt{51,84}=7,2\left(cm\right)\)
=>HC=BC-HB=12,8(cm)
Vì CD<CH
nên D nằm giữa C và H
=>CD+DH=CH
=>\(DH=12.8-\dfrac{80}{7}=\dfrac{48}{35}\left(cm\right)\)
ΔAHD vuông tại H
=>\(AH^2+HD^2=AD^2\)
=>\(AD^2=\left(\dfrac{48}{35}\right)^2+9,6^2=\dfrac{4608}{49}\)
=>\(AD=\sqrt{\dfrac{4608}{49}}=\dfrac{48\sqrt{2}}{7}\left(cm\right)\)
Đúng 1
Bình luận (0)