Cho tam giác ABC vuông tại A, cạnh AB=2, AC=1. Tính các tỉ số lượng giác của góc C

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A , BC =10cm , cosB =0,8.
a) Tính các cạnh AB, AC
b) Tính các tỉ số lượng giác của góc C
Ta có:
\(cosB=\dfrac{AB}{BC}\Rightarrow AB=BC.cosB=10.0,8=8\left(cm\right)\)
\(AC=\sqrt{BC^2-AB^2}=6\left(cm\right)\)
b.
\(sinC=\dfrac{AB}{BC}=\dfrac{8}{10}=0,8\)
\(cosC=\dfrac{AC}{BC}=\dfrac{6}{10}=0,6\)
\(tanC=\dfrac{AB}{AC}=\dfrac{8}{6}=\dfrac{4}{3}\)
\(cotC=\dfrac{AC}{AB}=\dfrac{3}{4}\)
Đúng 0
Bình luận (0)
Cho tám giác ABC vuông tại A, cạnh AB=2, AC=1. Tính các tỉ số lượng giác của góc C
Bài 1 : cho tam giác ABC vuông tại A , AB = 6 , góc B = alpha, biết tan alpha bằng 5/2 . Tính : a, Cạnh AC b, Cạnh BC Bài 2 : Cho tam giác MNP vuông tại P . Hãy viết các tỉ số lượng giác của góc M và góc N . Biết góc M = 40° .
Bài 1:
a) Ta có:
\(tanB=\dfrac{AC}{AB}\Rightarrow\dfrac{AC}{AB}=\dfrac{5}{2}\)
\(\Rightarrow AC=\dfrac{AB\cdot5}{2}=\dfrac{6\cdot5}{2}=15\)
b) Áp dụng Py-ta-go ta có:
\(BC^2=AB^2+AC^2=6^2+15^2=261\)
\(\Rightarrow BC=\sqrt{261}=3\sqrt{29}\)
Đúng 2
Bình luận (0)
Bài 2:
\(\left\{{}\begin{matrix}sinM=sin40^o\approx0,64\Rightarrow cosN\approx0,64\\cosM=cos40^o\approx0,77\Rightarrow sinN\approx0,77\\tanM=tan40^o\approx0,84\Rightarrow cotN\approx0,84\\cotM=cot40^o\approx1,19\Rightarrow tanN\approx1,19\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A có cạnh AB = 5cm, cạnh huyền dài hơn AC là 1cm.
a, Tính các tỉ số lượng giác của các góc B và C.
b, Tìm số đo các góc của tam giác ABC.
đề 1:
Cho tam giác ABC vuông tại A, AH vuông góc BC,AB=30cm,AH=24cm.
a)tính BH?BC?
b)tính các tỉ số lượng giác của các góc của tam giác AHB
đề 2
cho tam giác ABC vuông tại A, AH vuông góc BC , HB=4cm, HC=9cm
a)tính các cạnh tam giác ABC
b)tính các góc của tam giác ABC
Câu 1:
a: ΔAHB vuông tại H
=>\(AB^2=AH^2+HB^2\)
=>\(BH^2=30^2-24^2=\left(30-24\right)\left(30+24\right)=6\cdot54=6\cdot6\cdot9=6^2\cdot3^2=18^2\)
=>BH=18(cm)
Xét ΔABC vuông tại A có AH là đường cao
nên \(BH\cdot BC=BA^2\)
=>\(18\cdot BC=30^2=900\)
=>\(BC=\frac{900}{18}=50\left(\operatorname{cm}\right)\)
b: Xét ΔHAB vuông tại H có \(\sin HAB=cosB=\frac{HB}{AB}=\frac{18}{30}=\frac35\)
\(cosHAB=\sin B=\frac{AH}{AB}=\frac{24}{30}=\frac45\)
tan HAB=cot B\(=\frac{HB}{AH}=\frac{18}{24}=\frac34\)
cot HAB=tan B\(=\frac{AH}{HB}=\frac{24}{18}=\frac43\)
Bài 2:
a: BH+HC=BC
=>BC=4+9=13(cm)
Xét ΔABC vuông tại A có AH là đường cao
nên \(BH\cdot BC=BA^2\)
=>\(BA^2=4\cdot13=52\)
=>\(BA=\sqrt{52}=2\sqrt{13}\left(\operatorname{cm}\right)\)
ΔCAB vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC^2=13^2-\left(2\sqrt{13}\right)^2=169-52=117\)
=>\(AC=3\sqrt{13}\left(\operatorname{cm}\right)\)
b: Xét ΔABC vuông tại A có sin C\(=\frac{AB}{BC}=\frac{2\sqrt{13}}{13}\)
nên \(\hat{C}\) ≃34 độ
ΔABC vuông tại A
=>\(\hat{B}+\hat{C}=90^0\)
=>\(\hat{B}=90^0-34^0=56^0\)
Đúng 0
Bình luận (0)
Cho tam giác abc vuông tại a trong đó ab=8 ac=15 tính các tỉ số lượng giác của góc b rồi tính tỉ số lượng giác góc c
\(ab=8;ac=15\)
\(\Rightarrow\dfrac{b}{c}=\dfrac{8}{15}\)
\(tanB=\dfrac{b}{c}=\dfrac{8}{15}\Rightarrow cotB=\dfrac{1}{tanB}=\dfrac{15}{8}\left(tanB.cotB=1\right)\)
\(1+tan^2B=\dfrac{1}{cos^2B}\Rightarrow cos^2B=\dfrac{1}{1+tan^2B}\)
\(\Rightarrow cos^2B=\dfrac{1}{1+\dfrac{64}{225}}\dfrac{1}{\dfrac{289}{225}}=\dfrac{225}{289}\)
\(\Rightarrow cosB=\sqrt[]{\dfrac{225}{289}}=\dfrac{15}{17}\)
\(tanB=\dfrac{sinB}{cosB}\Rightarrow sinB=tanB.cosC=\dfrac{8}{15}.\dfrac{15}{17}\)
\(\Rightarrow sinB=\dfrac{8}{17}\)
Vì \(B+C=90^o\Rightarrow C=90^o-B\)
\(\Rightarrow\left\{{}\begin{matrix}sinC=cosB=\dfrac{15}{17}\\cosC=sinB=\dfrac{8}{17}\\tanC=cotB=\dfrac{15}{8}\\cotC=tanB=\dfrac{8}{15}\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Để tính các tỉ số lượng giác của góc B, ta sử dụng định nghĩa của các tỉ số lượng giác: sin(B) = cạnh đối diện / cạnh huyền = AC / AB = 15 / 8 cos(B) = cạnh kề / cạnh huyền = BC / AB = ? tan(B) = cạnh đối diện / cạnh kề = AC / BC = ? Để tính tỉ số lượng giác của góc C, ta sử dụng định nghĩa của các tỉ số lượng giác: sin(C) = cạnh đối diện / cạnh huyền = AB / AC = 8 / 15 cos(C) = cạnh kề / cạnh huyền = BC / AC = ? tan(C) = cạnh đối diện / cạnh kề = AB / BC = ? Tuy nhiên, để tính các tỉ số lượng giác của góc C, ta cần tìm giá trị của cạnh BC. Ta có thể sử dụng định lý Pythagoras trong tam giác vuông để tìm giá trị này: BC^2 = AC^2 - AB^2 BC^2 = 15^2 - 8^2 BC^2 = 225 - 64 BC^2 = 161 BC = √161 Sau đó, ta có thể tính các tỉ số lượng giác của góc B và góc C: sin(B) = 15 / 8 cos(B) = BC / AB = √161 / 8 tan(B) = 15 / √161 sin(C) = 8 / 15 cos(C) = BC / AC = √161 / 15 tan(C) = 8 / √161
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, AB = 6cm, AC = 8cm. Tính các tỉ số lượng giác của góc B, từ đó suy ra các tỉ số lượng giác của góc C.
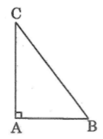
Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:
B C 2 = A B 2 + A C 2 = 6 2 + 8 2 = 100
Suy ra: BC = 10 (cm)
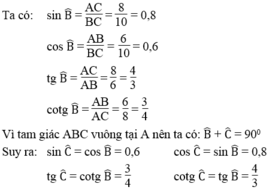
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A có AB = 6cm; AC = 8cm. Tính các tỉ số lượng giác của góc B, từ đó suy ra các tỉ số lượng giác của góc C
\(BC^2=AB^2+AC^2=36+64=100=10^2\)
\(\Rightarrow BC=10\left(cm\right)\)
\(SinB=\dfrac{AC}{BC}=\dfrac{8}{10}=\dfrac{4}{5}\Rightarrow SinC=Sin\left(90-B\right)=CosB=\dfrac{3}{5}\)
\(CosB=\dfrac{AB}{BC}=\dfrac{6}{10}=\dfrac{3}{5}\Rightarrow CosC=Cos\left(90-B\right)=SinB=\dfrac{4}{5}\)
\(tanB=\dfrac{AC}{AB}=\dfrac{8}{6}=\dfrac{4}{3}\Rightarrow tanC=tan\left(90-B\right)=CotB=\dfrac{3}{4}\)
\(CotB=\dfrac{AB}{AC}=\dfrac{6}{8}=\dfrac{3}{4}\Rightarrow cotC=cot\left(90-B\right)=tanB=\dfrac{4}{3}\)
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A có AB = 60mm, AC = 8cm. Tính các tỉ số lượng giác của góc B. Từ đó suy ra tỉ số lượng giác của góc C.
Đổi AB=60mm=6cm
Áp dụng định lí Pytago vào ΔBAC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Xét ΔABC có
\(\left\{{}\begin{matrix}\sin\widehat{B}=\dfrac{AC}{BC}=\dfrac{8}{10}=\dfrac{4}{5}\\\cos\widehat{B}=\dfrac{AB}{BC}=\dfrac{6}{10}=\dfrac{3}{5}\\\tan\widehat{B}=\dfrac{AC}{AB}=\dfrac{8}{6}=\dfrac{4}{3}\\\cot\widehat{B}=\dfrac{AB}{AC}=\dfrac{6}{8}=\dfrac{3}{4}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\sin\widehat{C}=\dfrac{AB}{BC}=\dfrac{6}{10}=\dfrac{3}{5}\\\cos\widehat{C}=\dfrac{AC}{BC}=\dfrac{8}{10}=\dfrac{4}{5}\\\tan\widehat{C}=\dfrac{AB}{AC}=\dfrac{6}{8}=\dfrac{3}{4}\\\cot\widehat{C}=\dfrac{AC}{AB}=\dfrac{8}{6}=\dfrac{4}{3}\end{matrix}\right.\)
Đúng 1
Bình luận (0)



















