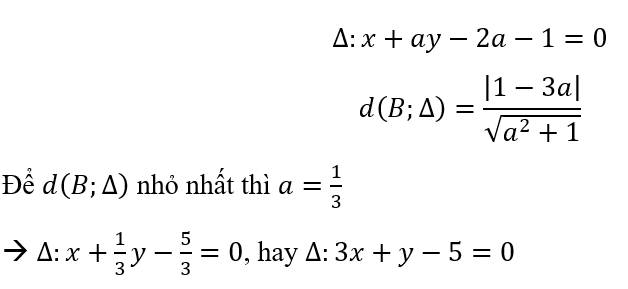cho 2 điểm A và B. trong tất cả các đường thẳng qua B, tìm đường thẳng có khoảng cách từ A đến nó là lớn nhất

Những câu hỏi liên quan
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng
∆
:
x
+
1
2
y
3
z
+
1
-
1
và hai điểm A(1; 2; -1); B (3; -1; -5). Gọi d là đường thẳng đi qua điểm A và cắt đường thẳng Δ sao cho khoảng cách từ điểm B đến đường thẳng d...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng ∆ : x + 1 2 = y 3 = z + 1 - 1 và hai điểm A(1; 2; -1); B (3; -1; -5). Gọi d là đường thẳng đi qua điểm A và cắt đường thẳng Δ sao cho khoảng cách từ điểm B đến đường thẳng d là lớn nhất. Phương trình đường thẳng d là:
A . x - 3 2 = y 2 = z + 5 - 1
B . x - 1 = y + 2 3 = z 4
C . x + 2 3 = y 1 = z - 1 - 1
D. Tất cả sai
Chọn D
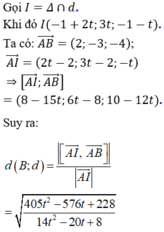
Xét hàm số:
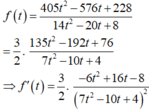
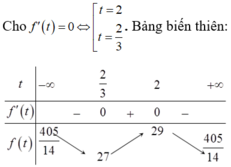
Do đó d (B; d) nhỏ nhất khi f(t) đạt giá trị nhỏ nhất bằng 27 tại t = 2/3. Suy ra ![]() . Chọn một vectơ chỉ phương của đường thẳng d là
. Chọn một vectơ chỉ phương của đường thẳng d là ![]()
Vậy phương trình đường thẳng ![]()
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz cho (P): x-2y+2z-50, A(-3;0;1), B(1;-1;3). Trong tất cả đường thẳng qua A song song với (P) viết phương trình đường thẳng d biết khoảng cách từ B đến d là lớn nhất.
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz cho (P): x-2y+2z-5=0, A(-3;0;1), B(1;-1;3). Trong tất cả đường thẳng qua A song song với (P) viết phương trình đường thẳng d biết khoảng cách từ B đến d là lớn nhất.
![]()
![]()
![]()
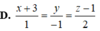
Trong không gian với hệ tọa độ Oxyz cho
(
P
)
:
x
-
2
y
+
2
z
-
5
0
, A(-3;0;1), B(1;-1;3). Trong tất cả đường thẳng qua A song song với (P) viết phương trình đường thẳng d biết khoảng cách từ B đến d là lớn nhất A.
x
+
3
-
2...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz cho ( P ) : x - 2 y + 2 z - 5 = 0 , A(-3;0;1), B(1;-1;3). Trong tất cả đường thẳng qua A song song với (P) viết phương trình đường thẳng d biết khoảng cách từ B đến d là lớn nhất
A. x + 3 - 2 = y 6 = z - 1 7
B. x - 3 - 2 = y 6 = z - 1 7
C. x + 3 - 2 = y 6 = z + 1 7
D. x + 3 - 2 = - y 6 = z - 1 7
Chọn A
Khoảng cách từ B đến đường thẳng d là lớn nhất nếu AB vuông góc với d.
Đường thẳng d qua A và nhận vecto chỉ phương là A B → ; n → với n ⇀ là vecto pháp tuyến của mặt phẳng (P).
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, cho các điểm A(1;2), B(2;-1). Đường thẳng đenta đi qua điểm A, sao cho khoảng cách từ điểm B đến đường thẳng đenta nhỏ nhất có phương trình là?
Cho đường thẳng (d) : y = 2x + 3
a) Tính khoảng cách từ điểm A(1; 2) đến đường thẳng (d)
b) Tính diện tích tam giác tạo bởi (d) với các trục tọa độ
c) Viết phương trình đường thẳng (∆) đi qua A sao cho khoảng cách từ O đến ∆ là lớn nhất, nhỏ nhất
Trong không gian Oxyz cho bốn điểm A(3;0;0),B(0;2;0),C(0;0;6) và D(1;1;1) Gọi ∆ là đường thẳng đi qua D và thỏa mãn tổng khoảng cách từ các điểm A,B,C đến ∆ là lớn nhất, hỏi ∆ đi qua điểm nào trong các điểm dưới đây? A. M(5;7;3) B. M(3;4;3) C. M(7;13;5) D. M(-1;-2;1)
Đọc tiếp
Trong không gian Oxyz cho bốn điểm A(3;0;0),B(0;2;0),C(0;0;6) và D(1;1;1) Gọi ∆ là đường thẳng đi qua D và thỏa mãn tổng khoảng cách từ các điểm A,B,C đến ∆ là lớn nhất, hỏi ∆ đi qua điểm nào trong các điểm dưới đây?
A. M(5;7;3)
B. M(3;4;3)
C. M(7;13;5)
D. M(-1;-2;1)
Phương trình mặt phẳng (ABC) là x 3 + y 2 + z 6 = 1 →2x+3y+z-6=0
Dễ thấy D ϵ (ABC). Gọi H,K,I lần lượt là hình chiếu của A,B,C trên ∆.
Do ∆ là đường thẳng đi qua D nên AH≤ AD,BK≤ BD,CI≤ CD.
Vậy để khoảng cách từ các điểm A,B,C đến ∆ là lớn nhất thì ∆ là đường thẳng đi qua D và vuông góc với (ABC). Vậy phương trình đường thẳng ∆ là x = 1 + 2 t y = 1 + 3 t ( t ∈ ℝ ) z = 1 + t . Kiểm tra ta thấy điểm M(5;7;3) ϵ ∆
Đáp án A
Đúng 0
Bình luận (0)
cho đường thẳng y=(m-2) x+2 (d) a, CMR: đường thẳng (d) luôn đi qua 1 điểm cố định với mọi m b,tìm già trị của m để khoảng cách từ gốc tọa độ đến đương thẳng (d) =1 c, tìm giá trị của m để khoảng cách từ gốc tọa độ đến đường thẳng m là lớn nhất
\(a,\) Gọi điểm cố định (d) luôn đi qua là \(A\left(x_0;y_0\right)\)
\(\Leftrightarrow y_0=\left(m-2\right)x_0+2\Leftrightarrow mx_0-2x_0+2-y_0=0\\ \Leftrightarrow\left\{{}\begin{matrix}x_0=0\\2-2x_0-y_0=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_0=0\\y_0=2\end{matrix}\right.\Leftrightarrow A\left(0;2\right)\)
Vậy \(A\left(0;2\right)\) là điểm cố định mà (d) lun đi qua
\(b,\) PT giao Ox,Oy: \(y=0\Leftrightarrow x=\dfrac{2}{2-m}\Leftrightarrow B\left(\dfrac{2}{2-m};0\right)\Leftrightarrow OB=\dfrac{2}{\left|m-2\right|}\\ x=0\Leftrightarrow y=2\Leftrightarrow C\left(0;2\right)\Leftrightarrow OC=2\)
Gọi H là chân đường cao từ O đến (d) \(\Leftrightarrow OH=1\)
Áp dụng HTL: \(\dfrac{1}{OH^2}=1=\dfrac{1}{OB^2}+\dfrac{1}{OC^2}=\dfrac{\left(m-2\right)^2}{4}+\dfrac{1}{4}\)
\(\Leftrightarrow m^2-4m+4+1=4\\ \Leftrightarrow m^2-4m+1=0\\ \Leftrightarrow\left[{}\begin{matrix}m=2+\sqrt{3}\\m=2-\sqrt{3}\end{matrix}\right.\)
\(c,\) Áp dụng HTL: \(\dfrac{1}{OH^2}=\dfrac{1}{OC^2}+\dfrac{1}{OB^2}=\dfrac{\left(m-2\right)^2}{4}+\dfrac{1}{4}\)
Đặt \(OH^2=t\)
\(\Leftrightarrow\dfrac{1}{t}=\dfrac{m^2-4m+5}{4}\Leftrightarrow t=\dfrac{4}{\left(m-2\right)^2+1}\le\dfrac{4}{0+1}=4\\ \Leftrightarrow OH\le2\\ OH_{max}=2\Leftrightarrow m=2\)
Đúng 1
Bình luận (0)
Cho đường thẳng
∆
:
x
+
1
2
y
3
z
+
1
-
1
và hai...
Đọc tiếp
Cho đường thẳng ∆ : x + 1 2 = y 3 = z + 1 - 1 và hai điểm A(1;2;-1), B(3;-1;-5) . Gọi d là đường thẳng đi qua điểm A và cắt đường thẳng sao cho khoảng cách từ B đến đường thẳng d là lớn nhất. Phương trình của d là:
A. x - 3 2 = y 2 = z + 5 - 1
B. x - 1 = y + 2 3 = z 4
C. x + 2 3 = y 1 = z - 1 - 1
D. x - 1 1 = y - 2 2 = z + 1 - 1
Đáp án là D.
![]()
Ta có:
![]()
![]()
![]()
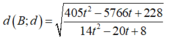
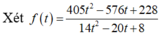
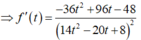

![]()
Đường thẳng d đi qua A(1;2;-1) và có VTCP
![]()
Đúng 0
Bình luận (0)
cho đường thẳng (m - 2) x + y = 3
a) chứng minh rằng đường thẳng đi qua điểm cố định. Tìm điểm cố định đó
b) Tìm m để khoảng cách từ O đến đường thẳng là lớn nhất. Tim phương trình đường thẳng