Cho \(\Delta ABC\) có các đường trung tuyến AM; BN; CP. C/minh: \(AM+BN+CP< AB+BC+AC\)

Những câu hỏi liên quan
Cho Delta ABC có các trung tuyến AM;BN;CP cắt nhau tại trọng tâm G. Trên tia AM lấy D sao cho G là trung điểm của AD.a/ C.m các cạnh của BGD 2/3 các trung tuyến của DeltaABCb/ C.m các trung tuyến của DeltaBGD1/2 các cạnh của tam giác ABC c/ Nêu cách dựng tam giác ABC khi biết độ dài 3 đường trung tuyến AM;BN;CP
Đọc tiếp
Cho \\(\Delta ABC\) có các trung tuyến AM;BN;CP cắt nhau tại trọng tâm G. Trên tia AM lấy D sao cho G là trung điểm của AD.
a/ C.m các cạnh của BGD= 2/3 các trung tuyến của \(\Delta\)ABC
b/ C.m các trung tuyến của \(\Delta\)BGD=1/2 các cạnh của tam giác ABC
c/ Nêu cách dựng tam giác ABC khi biết độ dài 3 đường trung tuyến AM;BN;CP
Hình tự vẽ
a) Ta có :
AG = GD . Mà GM = \(\frac{1}{2}\) AG
=> GD = \(\frac{1}{2}\) AG
Do AG = \(\frac{1}{3}\) AM
=> GD = \(\frac{2}{3}\) AM (*)
Xét tứ giác GBDC ta có:
BM = MC ( gt ) (1)
GM= MD ( do GD = \(\frac{1}{2}\) AG ) (2)
Từ (1)(2) => Tứ giác GBDC là hình bình hành
=> GC// và =BD ; BG // và =DC
Xét tam giác ABD ta có:
AP = P B ( gt ) ( 3)
AG = GD ( gt ) (4)
Từ (3)(4) => PG là đường trung bình của tam giác ABD
=> PG = \(\frac{1}{2}\)BD .Do BD = GC => PG=\(\frac{1}{2}\)GC
Mà PG = \(\frac{1}{3}\)PC => GC =\(\frac{2}{3}\)PC(**)
Chứng mình tương tự . Xét tam giác ADC ( làm tường tự cái trên nha )
=> NG=\(\frac{2}{3}\)BN (***)
Từ (*)(**)(***) => Đpcm
Đúng 0
Bình luận (0)
b) Xét tam giác DBA ta có :
AG = GD ( gt )
BF=FD ( gt )
=> GF là đường trung bình bình của tam giác DAB
=> GF = \(\frac{1}{2}\)AB( 5)
Ta có : DC = GB ( cm ở câu a )
Do BE = EG ; BG =\(\frac{2}{3}\)BN ( cm ở câu a)
=> EN = BG => EN= DC
Mà BG// DC ( cm ở câu a)
=> tứ giác ENCD là hình bình hành ( 1 cặp cạnh // và bằng nha )
=> DE=NC
Mà NC =\(\frac{1}{2}\)AC (6)
=> AN= NC
Ta lại có BM=MC ( gt) => BI=\(\frac{1}{2}\)BC (7)
Từ (5)(6)(7) => Đpcm
Đúng 0
Bình luận (0)
c / tự làm đi nha câu này dài t nhác làm
Đúng 0
Bình luận (0)
ChoDelta ABC, đường trung tuyến AM. Các tia phân giác của các góc AMB, AMC cắt AB, AC theo thứ tự ở D và E.a. cmr DE//BCb. Cho BCa, AMm. Tính DEc. Giao điểm I của Am và DE chuyển động trên đường nào nếu Delta ABCcó BC cố định, AMm không đổid. Delta ABCcó điều kiện gì để DE là đường trung bình của Delta ABC
Đọc tiếp
Cho\(\Delta ABC\), đường trung tuyến AM. Các tia phân giác của các góc AMB, AMC cắt AB, AC theo thứ tự ở D và E.
a. cmr DE//BC
b. Cho BC=a, AM=m. Tính DE
c. Giao điểm I của Am và DE chuyển động trên đường nào nếu \(\Delta ABC\)có BC cố định, AM=m không đổi
d. \(\Delta ABC\)có điều kiện gì để DE là đường trung bình của \(\Delta ABC\)
Cho \(\Delta ABC\), đường trung tuyến AM. Tia phân giác \(\widehat{AMB}\) cắt AB tại D, tia phân giác \(\widehat{AMC}\) cắt AC tại E. Gọi I là giao điểm của AM và DE. Hỏi \(\Delta ABC\) cần có điều kiện gì để DE là đường trung bình của \(\Delta ABC\)?
AD/DB=AM/MB
AE/EC=AM/MC
mà MB=MC
nên AD/DB=AE/EC
=>DE//BC
Để DE là đừog trung bình của ΔABC thì AD/DB=AE/EC=1
=>AM/MB=AM/MC=1
=>ΔABC vuông tại A
Đúng 2
Bình luận (0)
Cho \(\Delta\)ABC,các đường trung tuyến AM,BE,CF cắt nhau tại G
a)Chứng minh:S\(\Delta\)BAG=\(\dfrac{1}{3}\)S\(\Delta\)ABC
b)Chứng minh S\(\Delta\)ABG=S\(\Delta\)ACG=S\(\Delta\)BCG
Cho \(\Delta ABC\)có đường cao AH và đường trung tuyến AM chia \(\widehat{A}\)thành 3 góc bằng nhau. Tính các góc của \(\Delta ABC\)
Cho tam giác ABC có AB AC 5cm, BC6cm . đường trung tuyến AM xuất phát từ đỉnh A của tam giác ABCa) Chứng minh Delta AMBDelta AMC và AM là tia phân của góc Ab) Chứng minh AM perp BCc) Tính độ dài các đoạn thẳng BM và AMd) Từ M vẽ ME perp AB ( E thuộc AB ) và MF perp AC ( F thuộc AC ) . Tam giác MEF là tam giác gì ? Vì saoai làm được mình cho 10000 sao
Đọc tiếp
Cho tam giác ABC có AB = AC = 5cm, BC=6cm . đường trung tuyến AM xuất phát từ đỉnh A của tam giác ABC
a) Chứng minh \(\Delta AMB=\Delta AMC\) và AM là tia phân của góc A
b) Chứng minh AM \(\perp\) BC
c) Tính độ dài các đoạn thẳng BM và AM
d) Từ M vẽ ME \(\perp\) AB ( E thuộc AB ) và MF \(\perp\) AC ( F thuộc AC ) . Tam giác MEF là tam giác gì ? Vì sao
ai làm được mình cho 10000 sao
a) Xét ΔABC có AB=AC=5
=> ΔABC cân tại A
ta có AM là trung tuyến => AM là đường phân giác của góc A (tc Δ cân)
=>\(\widehat{B}=\widehat{C}\)(tc)
Xét ΔABM và ΔACM có
AB=AC gt
có AM là trung tuyến => BM=CM
\(\widehat{B}=\widehat{C}\) (cmt)
=>ΔABM = ΔACM (cgc)
b) có ΔABC cân
mà AM là trung tuyến => AM là đường cao (tc Δ cân)
c) ta có AM là trung tuyến =>
M là trung điểm của BC
=> BM=CM=\(\dfrac{BC}{2}=\dfrac{6}{2}=3\)cm
Xét ΔABM có AM là đường cao => \(\widehat{AMB}=\)90o
=> AM2+BM2=AB2
=> AM2+32=52
=> AM =4 cm
d) Xét ΔBME và ΔCMF có
\(\widehat{MEB}=\widehat{MFC}=\)90o (ME⊥AB,MF⊥AC)
BM=CM (cmt)
\(\widehat{B}=\widehat{C}\)
=>ΔBME = ΔCMF (ch-cgv)
=>EM=FM( 2 góc tương ứng)
Xét ΔMEF có
EM=FM (cmt)
=> ΔMEF cân tại M
Đúng 2
Bình luận (1)
ai giúp mik bài này đc ko plsssssssssssssssss
Đúng 1
Bình luận (1)
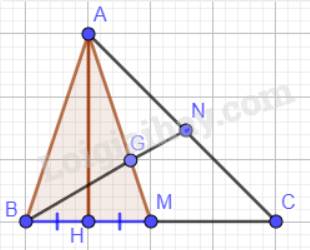
Cho tam giác ABC có hai đường trung tuyến AM và BN cắt nhau tại G. Gọi H là hình chiếu của A lên đường thẳng BC. Giả sử H là trung điểm của đoạn thẳng BM. Chứng minh:
a) \(\Delta AHB = \Delta AHM\); b) \(AG = \dfrac{2}{3}AB\).
a) Xét tam giác AHB và tam giác AHM có:
AH chung;
\(\widehat {AHB} = \widehat {AHM}\)(H là hình chiếu của A lên BC nên \(AH \bot BC\));
HB = HM (H là trung điểm của BM).
Vậy \(\Delta AHB = \Delta AHM\)(c.g.c).
b) \(\Delta AHB = \Delta AHM\)nên AB = AM ( 2 cạnh tương ứng).
G là giao điểm của hai đường trung tuyến AM và BN nên G là trọng tâm tam giác ABC. Nên: \(AG = \dfrac{2}{3}AM\).
Mà AB = AM suy ra: \(AG = \dfrac{2}{3}AB\).
Đúng 0
Bình luận (0)
BT: Cho ΔABC có AM là đường trung tuyến
đồng thời là đường cao
C/m: ΔABC cân ở A
Cm: a) Xét t/giác ABM và t/giác ACM
có AM : chung
góc AMB = góc AMC = 900 (gt)
BM = CM (gt)
=> t/giác ABM = t/giác ACM (c.g.c)
=> AB = AC (hai cạnh tương ứng)
=> t/giác ABC cân tạiA
Đúng 0
Bình luận (0)
Ta có AM là đường trung tuyến vậy suy ra MB = MC
Xét ⚠️ BAM và ⚠️ CAM có:
MB = MC( Cmt)
Góc AMC=Góc AMB=90 độ
AM cạnh chung
Suy ra ⚠️ BAM = ⚠️ CAM( c-g-c )
suy ra AB =AC (vì ⚠️ BAM = ⚠️ CAM)
suy ra ⚠️ ABC cân tại A
Đúng 1
Bình luận (0)
Cho \(\Delta ABC\) có các đường trung tuyến AM, BN, CP.
C/minh: \(\dfrac{3}{4}\left(AB+BC+CA\right)< AM+BN+CP< AB+BC+CA\)
Trên tia đối của tia MA lấy điểm D sao cho MA = MD
Dễ dàng chứng minh t/g ABM = t/g DCM (c.g.c) => AB = CD
Xét t/g ACD có: AD < AC + CD
=> 2AM < AC + AB => AM < \(\frac{AB+AC}{2}\)
Chứng minh tương tự ta có: \(BN< \frac{AB+BC}{2};CF< \frac{CA+CB}{2}\)
\(\Rightarrow AM+BN+CP< \frac{AB+AC+AB+BC+CA+CB}{2}=\frac{2\left(AB+AC+BC\right)}{2}=AB+AC+BC\) (1)
Gọi trọng tâm là G
Xét t/g GBC có: GB + GC > BC => \(\frac{2}{3}BN+\frac{2}{3}CP>BC\) => \(BN+CP>\frac{3}{2}BC\)
Tương tự ta có: \(AM+CP>\frac{3}{2}AC;AM+BN>\frac{3}{2}AB\)
=> BN + CP + AM + CP + AM + BN > \(\frac{3}{2}BC+\frac{3}{2}AC+\frac{3}{2}AB\)
=> 2(AM + BN + CP) > \(\frac{3}{2}\left(AB+BC+AC\right)\)
=> AM + BN + CP > \(\frac{3}{4}\left(AB+BC+AC\right)\) (2)
Từ (1) và (2) => \(\frac{3}{4}\left(AB+BC+AC\right)< AM+BN+CP< AB+BC+AC\) (đpcm)
Đúng 0
Bình luận (0)




















