a) 3(2a - 1) + 5(3 - a)

= 6a - 3 + 15 -5a

= a + 12

Thay a=\(-\frac{3}{2}\) vào biểu thức a) ta có:

⇒ \(-\frac{3}{2}+12=\frac{21}{2}\)

b) 25x - 4(3x - 1) + 7(5 - 2x)

= 25x -12x + 4 + 35 - 14x

= -x + 39

Thay x= 2,1 vào biểu thức b) ta có:

⇒ -2,1 + 39 = 36,9

c) 4a - 2(10a - 1) + 8a - 2

= 4a -20a + 2 + 8a - 2

= -8a

Thay a= -0,2 vào biểu thức c) ta có:

⇒ -8.(-0,2)= 1,6

d) 12(2 - 3b) + 35b - 9(b + 1)

= 24 - 36b + 35b - 9b -9

= 15 - 10b

Thay b=\(\frac{1}{2}\) vào biểu thức d) ta có:

⇒ 15 - 10. \(\frac{1}{2}=\) 10

\(a,a=-\dfrac{3}{2}\)

\(\Rightarrow3\left[2\left(-\dfrac{3}{2}\right)-1\right]+5\left(3+\dfrac{3}{2}\right)=3.\left(-3-1\right)+5.\dfrac{9}{2}=-12+\dfrac{45}{2}=\dfrac{21}{2}\)

\(b,x=2,1\)

\(\Rightarrow25.2,1-4\left(3.2,1-1\right)+7\left(5-2.2,1\right)=52,5-4.5,3+7.0,8=36,9\)

\(c,b=\dfrac{1}{2}\)

\(\Rightarrow12\left(2-3.\dfrac{1}{2}\right)+35.\dfrac{1}{2}-9\left(\dfrac{1}{2}+1\right)=12.\dfrac{1}{2}+\dfrac{35}{2}-9.\dfrac{3}{2}=6+\dfrac{35}{2}-\dfrac{27}{2}=10\)

\(d,a=-0,2\)

\(\Rightarrow4.\left(-0,2\right)^2-2\left(10.\left(-0,2\right)-1\right)+4.\left(-0,2\right)\left(2-\left(-0,2\right)^2\right)\)

\(=4.0,04-2.\left(-3\right)-0,8.1,96\)

\(=0,16+6-1,568\)

\(=4,592\)

a: A=6a-3+15-5a=a+12

Khi a=-3/2 thì A=-3/2+12=10,5

b: B=25x-12x+4+35-8x=5x+39

Khi x=2,1 thì B=10,5+39=49,5

c: C=24-6b+35b-9b-9=20b+15

Khi b=0,5 thì C=10+15=25

d: D=4a^2-20a+2+8a-4a^3=-4a^3+4a^2-12a+2

Khi a=-0,2 thì 

D=-4*(-1/5)^3+4*(-1/5)^2-12*(-1/5)+2=4,592

4a² - 2(10a - 1) + 4a(2 - a⁵)

= 4a² - 20a + 2 + 8a - 4a⁶

= 4a⁶ + 4a² - 12a + 2

Thay a = -0,2 vào biểu thức trên ta được:

4.(-0,2)⁶ + 4.(-0,2)² - 12.(-0,2) + 2

= 0,000256 + 1,6 + 2,4 + 2

= 6,000256

Ta có : 3(2a - 1) + 5(3 - a)
=6a-3+15-a

=5a+12

Với a=-3/2

=>5a+12=5 . (-3/2) +12 = -15/2+24/2=9/2

a.

Với a = \(\frac{-3}{2}\)thì thay vào ta có :

3 ( 2a - 1 ) + 5 ( 3 - a )     

= 3 ( 2 . \(\frac{-3}{2}\)- 1 ) + 5 . ( 3 - \(\frac{-3}{2}\))

= 3 . ( - 3 - 1 ) + 5 . 4,5

= 3 . ( - 4 ) + 22,5

= - 12 + 22,5

= 10,5

b.

Với x = 2,1 thì thay vào ta có :

 25x - 4( 3x - 1 ) + 7 ( 5 - 2x )

= 25 . 2,1 - 4 . ( 3 . 2,1 - 1 ) + 7 . ( 5 - 2 . 2,1 )

= 52,5 - 4 . ( 6,3 - 1 ) + 7 . ( 5 - 4 ,1 )

= 52,5 - 4 . 5,3  + 7 . 1,1

= 52,5 - 21,2 + 7 ,7

= 31,3 + 7 ,7 

= 39

c.

Với a = - 0,2 thì thay vào ta có :

4a - 2(10a - 1) + 8a - 2

= 4 . ( - 0,2 ) . [ 10 . ( - 0,2 ) - 1 ] + 8. ( - 0,2 ) - 2

= - 0,8 . ( - 2 - 1 ) + (- 1,6 ) - 2

= - 0,8 . ( - 3 ) + ( - 1,6 ) - 2

= 2,4 + ( - 1 , 6 ) - 2

= 0,8 - 2

= - 1,2

Đặt a/3=b/5=k

=>a=3k; b=5k

\(B=\dfrac{5\cdot9k^2+3\cdot25k^2}{10\cdot9k^2-3\cdot25k^2}=8\)

Bài 1 : 

\(N=\left(x+y\right)\left(y+z\right)\left(x+z\right)\)

Ta có : \(x+y+z=0\Rightarrow x+y=-z;y+z=-x;x+z=-y\)

hay \(-z.\left(-x\right)\left(-y\right)=-zxy\)

mà \(xyz=2\Rightarrow-xyz=-2\)

hay N nhận giá trị -2 

Bài 2 : 

\(\frac{a}{b}=\frac{10}{3}\Rightarrow\frac{a}{10}=\frac{b}{3}\)Đặt \(a=10k;b=3k\)

hay \(\frac{30k-6k}{10k-9k}=\frac{24k}{k}=24\)

hay biểu thức trên nhận giá trị là 24 

c, Ta có : \(a-b=3\Rightarrow a=3+b\)

hay \(\frac{3+b-8}{b-5}-\frac{4\left(3+b\right)-b}{3\left(3+b\right)+3}=\frac{-5+b}{b-5}-\frac{12+4b-b}{9+3b+3}\)

\(=\frac{-5+b}{b-5}-\frac{12+3b}{6+3b}\)quy đồng lên rút gọn, đơn giản rồi 

1.Ta có:\(x+y+z=0\)

\(\Rightarrow\hept{\begin{cases}x+y=-z\\y+z=-x\\x+z=-y\end{cases}}\)

\(\Rightarrow N=\left(x+y\right)\left(y+z\right)\left(x+z\right)=\left(-z\right)\left(-x\right)\left(-y\right)=-2\)

2.Ta có:\(\frac{a}{b}=\frac{10}{3}\Rightarrow\frac{a}{10}=\frac{b}{3}\)

Đặt \(\frac{a}{10}=\frac{b}{3}=k\Rightarrow a=10k;b=3k\)

Ta có:\(A=\frac{3a-2b}{a-3b}=\frac{3.10k-2.3k}{10k-3.3k}=\frac{30k-6k}{10k-9k}=\frac{k\left(30-6\right)}{k\left(10-9\right)}=24\)

Vậy....

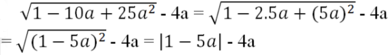
Tại a = √2 ta được:

= |1 - 5√2| - 4√2

= (5√2 - 1) - 4√2

= √2 - 1