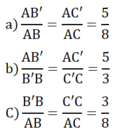Trên ba cạnh AB; AC: BC của tam giác đều ABC . Lấy các điểm theo thứ tự M; N; P sao cho AM = BN = CP. Gọi O là giao điểm 3 đường trung trực của \(\Delta ABC\). C/minh O cũng là giao điểm ba đường trung trực của \(\Delta MNP\).

Những câu hỏi liên quan
Vẽ tam giác ABC trên giấy kẻ học sinh như trên hình 3. Dựng đường thẳng a song song với cạnh BC, cắt hai cạnh AB, AC theo thứ tự tại B và C. Đường thẳng a định ra trên cạnh AB ba đoạn thẳng AB, BB và AB, và định ra trên cạnh AC ba đoạn thẳng tương ứng là AC, CC và AC. So sánh các tỉ số:
Đọc tiếp
Vẽ tam giác ABC trên giấy kẻ học sinh như trên hình 3. Dựng đường thẳng a song song với cạnh BC, cắt hai cạnh AB, AC theo thứ tự tại B' và C'.
Đường thẳng a định ra trên cạnh AB ba đoạn thẳng AB', B'B và AB, và định ra trên cạnh AC ba đoạn thẳng tương ứng là AC', C'C và AC.
So sánh các tỉ số:
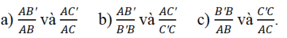
Cho tam giác ABC, M nằm trên cạnh BC.
a, so sánh MA với AB+BM
b, MA+MC<BA+BC
c, cho D nằm trên cạnh AM. C/m: DA+DC<MA+MC; DA+DC<BA+BC
Cho tam giác ABC có ba cạnh AB = 14cm, AC = 20cm và BC = 18cm. Trên cạnh AB lấy điểm E sao cho AE = 10cm. Trên cạnh AC lấy điểm D sao cho AD = 7cm.
a/ Chứng minh tam giác ADE ~ tam giác ABC
b/ Tính DE
Hình bạn tự vẽ ạ.
a, Xét \(\Delta ADE\) và \(\Delta ABC\) có :
\(\dfrac{AD}{AB}=\dfrac{7}{14}=\dfrac{1}{2}\)
\(\dfrac{AE}{AC}=\dfrac{10}{20}=\dfrac{1}{2}\)
\(\Rightarrow\dfrac{AD}{AB}=\dfrac{AE}{AC}\left(=\dfrac{1}{2}\right)\)
Mà \(\widehat{A}:chung\)
\(\Rightarrow\Delta ADE\sim\Delta ABC\left(c-g-c\right)\)
b, Ta có : \(\Delta ADE\sim\Delta ABC\left(cmt\right)\)
\(\Rightarrow\dfrac{AD}{AB}=\dfrac{ED}{BC}\)
hay \(\dfrac{7}{14}=\dfrac{ED}{18}\)
\(\Rightarrow ED=\dfrac{7.18}{14}=9\left(cm\right)\)
Đúng 0
Bình luận (0)
gọi O là giao điểm ba đường trung trực của ba cạnh tam giác ABC. Tia AO cắt BC tại D. Trên cạnh AB lấy điêm E sao cho DE =DB; tên cạnh AC lấy điểm F sao cho Df=Dc
CMRa) Hk song song AB.
b) AC*BD=AB*CD+AD*BC
Cho hình bình hành ABCD.Lấy điểm E trên cạnh AB, điểm F trên cạnh CD sao cho AE=CF. CMR: ba đường thẳng AC,BD,EF đồng quy
Cho hình vẽ:
Vì ABCD là hình bình hành
\(\Rightarrow\)AB // CD hay AE // CF
Lại có: AE = CF ( gt ).
Suy ra: AECF là hình bình hành
\(\Rightarrow\)AE, CF cắt nhau tại trung điểm mỗi đường
Hay \(AC\in O;CF\in O\) (1)
Mà AC và BD cũng cắt nhau tại trung điểm mỗi đường
\(\Rightarrow AC\in O;BD\in O\)( 2 )
Từ ( 1 ) và ( 2 ) suy ra ba đường thẳng AC, BD, EF đồng quy ( đpcm )
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD. Lấy điểm E trên cạnh AB, điểm F trên cạnh CD sao cho AE = CF. Chứng minh rằng ba đường thẳng AC, BD, EF đồng quy.
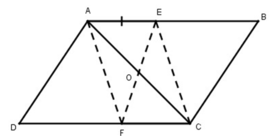
Gọi O là giao điểm của hai đường chéo AC và BD.
Xét tứ giác AECF:
AB // CD (gt)
⇒ AE // CF
AE = CF (gt)
Suy ra: Tứ giác AECF là hình bình hành ( vì có một cặp cạnh đối song song và bằng nhau)
⇒ AC và EF cắt nhau tại trung điểm mỗi đường
OA = OC ( tính chất hình bình hành) ⇒ EF đi qua O
Vậy AC, BD, EF đồng quy tại O.
Đúng 0
Bình luận (0)
Cho tam ABC có AB < AC. Tia phân giác góc A cắt cạnh BC tại D. Lấy cạnh E trên cạnh AC sao cho AE = AB. Trên tia đối của tia BA lấy điểm F sao cho BF = EC. Chứngminh rằng:
a) DB = BE
b) ΔBDF = ΔEDC
c) E, D, F thẳng hàng
a: Xét ΔABD và ΔAED có
AB=AE
góc BAD=góc EAD
AD chung
Do đó: ΔABD=ΔAED
=>DB=DE
b: Xét ΔDBF và ΔDEC có
DB=DE
góc DBF=góc DEC
BF=EC
Do đó: ΔDBF=ΔDEC
c: ΔDBF=ΔDEC
nên góc BDF=góc EDC
=>góc BDF+góc BDE=180 đọ
=>E,D,F thẳng hàng
Đúng 1
Bình luận (0)
Cho A', B', C' lần lượt nằm trên ba cạnh BC, AC, AB (hoặc nằm trên các đường thẳng chứa các cạnh của tam giác ABC) sao cho A', B', C' thẳng hàng. Chứng minh rằng :
\(\frac{AC'}{BC'}.\frac{BA'}{CA'}.\frac{CB'}{AB'}=1\) (Định lí Mênêlauýt).
Cho hình bình hành ABCD .Lấy điểm E trên cạnh AB,điểm F trên cạnh CD sao cho AE=CF .Chứng minh rằng ba đường thẳng AC,BD,EF đồng quy
Hình bình hành ABCD có :
AC cắt BD tại trung điểm của AC và BD ( 1 )
Hình bình hành EBFD có :
EF cắt BD tại trung điểm của EF và BD ( 2 )
\(\Rightarrow\)Từ ( 1 ) và ( 2 ) suy ra AC ; BD ; EF đồng quy
Đúng 0
Bình luận (0)
Cho ∆ ABC vuông tại A ( AB < AC ). Trên cạnh BC lấy điểm M sao cho BA = BM , kẻ BH ⊥ AM ( H∊ AM). Tia BH cắt cạnh BC tại E.
a) Giả sử AB= 8cm , BC = 10 cm . Tính độ dài cạnh AB
b) Chứng minh BE p/giác ABC
c) EM ⊥ BC
d) MB ∩ BA = {F} . chứng tỏ ∆ BFC cân
e) AM // FC