cho tứ giác abcd gọi k là trung điểm cạnh ab i là trung điểm cạnh cd biết cd=2ki chứng minh rằng ad+bc>=cd

Những câu hỏi liên quan
Cho tứ giác ABCD. Gọi K là trung điểm AB, I là trung điểm CD. Biết KI=1/2CD. CHứng minh: AD+BC≥CD
Cho hình thang cân ABCD ( AB//CD, AB<CD). Gọi O là giao điểm của 2 đoạn thẳng AD và BC.
a. Chứng minh tam giác OAN cân
b.Gọi I là trung điểm của AB, gọi K là trung điểm của CD. Chứng minh 3 điểm O,I,K thẳng hàng.
c.Qua điểm M thuộc cạnh AD. Kẻ đường thẳng song song với CD nó cắt BC tại N. Chứng minh MNCD là hthang cân.
cho hình thang cân ABCD (AB//CD) . Trên cạnh AB lấy trung điểm E , trên cạnh CD lấy trung điểm F
a)chứng minh tam giác AED=BEC
b)chứng minh EFvuong gốc CD
c) Gọi I là trung điểm của AD và BC . Chứng minh E,F,I thảng hàng
cho tứ giác abcd. gọi m, n, p, q lần lượt là trung điểm của các cạnh ab, bc, cd, da và i, k là trung điểm các đường chéo ac, bd. chứng minh rằng:
a) tứ giác mnpq, inkq là hình bình hành.
b) gọi o là giao điểm của mp, nq. chứng minh 3 điểm i, o, k thẳng hàng
các bạn giúp mình với ạ, mình cảm ơn rất nhiều!
a) Ta có:-
- M là trung điểm của AB
⇒ AM = MB.
- N là trung điểm của BC
⇒ BN = NC.
- P là trung điểm của CD
⇒ CP = PD.
- Q là trung điểm của DA
⇒ DQ = QA.
Do đó, ta có: AM = MB = BN = NC = CP = PD = DQ = QA.
⇒ tứ giác MNPQ là hình bình hành.
Có:
- I là trung điểm của AC
⇒AI = IC.
- K là trung điểm của BD
⇒ BK = KD.
Do đó, ta có: AI = IC = BK = KD.
⇒ tứ giác INKQ là hình bình hành.
b)Gọi O là giao điểm của MP và NQ ta có:
MP // AB và NQ//CD ( M và N là trung điểm của AB và CD).
⇒ MP song song với NQ.
do đó :O nằm trên MP và NQ.
Gọi H là giao điểm của MI và NK ta có:
MI // AC và NK // BD (do I và K là trung điểm của đường chéo AC và BD).
⇒ MI song song với NK.
Do đó: H nằm trên cả MI và NK.
Gọi G là giao điểm của OH và BD ta có:
OH //MP và BD // MP (do O nằm trên MP và NQ, và H nằm trên MI và NK).
⇒ OH song song với BD.
doo đó: G nằm trên OH và BD.
⇒ I, O, K thẳng hàng.(ĐPCM)
Đúng 1
Bình luận (0)
a: Xét ΔBAC có BM/BA=BN/BC=1/2
nên MN//AC và MN=1/2AC
Xét ΔDAC có DQ/DA=DP/DC
nên PQ//AC và PQ/AC=DQ/DA=1/2
=>PQ=1/2AC
=>MN//PQ và MN=PQ
=>MNPQ là hình bình hành
Xét ΔCAB có CI/CA=CN/CB=1/2
nên IN//AB và IN=1/2AB
Xét ΔDAB có DQ/DA=DK/DB=1/2
nên QK//AB và QK=1/2AB
=>IN//QK và IN=QK
=>INKQ là hình bình hành
b: MNPQ là hình bình hành
=>MP cắt NQ tại trung điểm của mỗi đường
=>O là trung điểm của NQ
INKQ là hbh
=>IK cắt NQ tại trung điểm của mỗi đường
=>I,O,K thẳng hàng
Đúng 0
Bình luận (0)
Cho hình thang ABCD
(
A
B
/
/
C
D
)
c
ó
A
B
A
D
C
D
/
2
.
Gọi M là trung điểm của CD và H là giao điểm của AM và BD.a) Chứng minh tứ giác ABMD là hình thoib) Chứng minh BD ⊥ BCc) Chứng minh ΔAHD và ΔCBD đồng dạngd) Biết A...
Đọc tiếp
Cho hình thang ABCD ( A B / / C D ) c ó A B = A D = C D / 2 . Gọi M là trung điểm của CD và H là giao điểm của AM và BD.
a) Chứng minh tứ giác ABMD là hình thoi
b) Chứng minh BD ⊥ BC
c) Chứng minh ΔAHD và ΔCBD đồng dạng
d) Biết AB = 2,5cm; BD = 4cm. Tính độ dài cạnh BC và diện tích hình thang ABCD.

a) Ta có: AB = AD = CD/2 và M là trung điểm của CD (gt)
⇔ AB = DM và AB // DM
Do đó tứ giác ABMD là hình bình hành có AB = AD. Vậy ABMD là hình thoi.
b) M là trung điểm của CD nên BM là trung tuyến của ΔBDC mà MB = MD = MC. Do đó ΔBDC là tam giác vuông tại B hay DB ⊥ BC
c) ABMD là hình thoi (cmt) ⇔ ∠D1 = ∠D2
Do đó hai tam giác vuông AHD và CBD đồng dạng (g.g)
d) Ta có :
![]()
Xét tam giác vuông AHB, ta có :

Dễ thấy tứ giác ABCM là hình bình hành (AB // CM và AB = CM)
⇒ BC = AM = 3 (cm)
Ta có:
![]()
M là trung điểm của DC nên
SBMD = SBMC = SBCD/2 = 3 (cm2) (chung đường cao kẻ từ B và MD = MC)
Mặt khác ΔABD = ΔMDB (ABCD là hình thoi)
⇔ SABD = SBMD = 3 (cm2)
Vậy SABCD = SABD + SBMD + SBMC = 9 (cm2)
Đúng 1
Bình luận (0)
Cho hình thang cân ABCD (AB//CD và AB<CD)
a) Gọi các điểm M, N, P, Q lần lượt là trung điểm các cạnh AB, BC, CD, DA. Chứng minh rằng MNPQ là hình thoi.
b) Trên cạnh CD lấy điểm E sao cho CE = AB. Chứng minh rằng AC là phân giác góc BCD thì tứ giác ABCE là hình thoi.
a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)
Đúng 0
Bình luận (0)
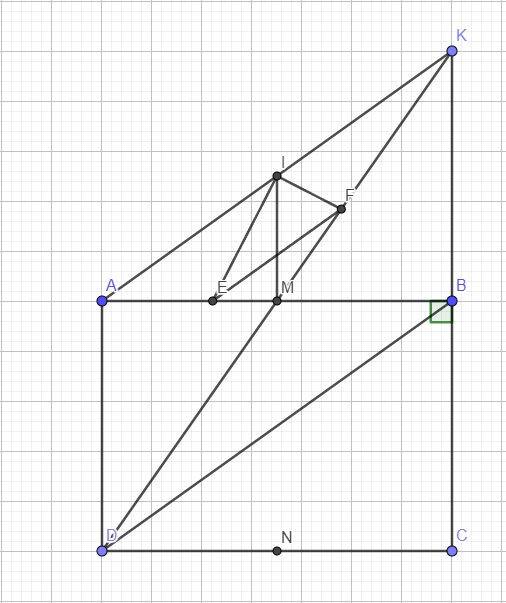
Cho hình chữ nhật ABCD(ABAD), gọi M là trung điểm cạnh AB. Từ M kẻ MN vuông góc với CD tại N( N thuộc CD) a, Trên tia DM lấy điểm K sao cho M là trung điểm của đoạn thẳng DK. Chứng minh tứ giác ADBK là hình bình hành và tam giác AKC cân. b,Gọi I là trung điểm của AK. Tia phân giác của góc AIM cắt AM tại E, tia phân giác của góc KIM cắt MK ở F. Chứng minh EF song song với BD.
Đọc tiếp
Cho hình chữ nhật ABCD(AB>AD), gọi M là trung điểm cạnh AB. Từ M kẻ MN vuông góc với CD tại N( N thuộc CD)
a, Trên tia DM lấy điểm K sao cho M là trung điểm của đoạn thẳng DK. Chứng minh tứ giác ADBK là hình bình hành và tam giác AKC cân.
b,Gọi I là trung điểm của AK. Tia phân giác của góc AIM cắt AM tại E, tia phân giác của góc KIM cắt MK ở F. Chứng minh EF song song với BD.
a: Xét tứ giác ADBK có
M là trung điểm chung của AB và DK
=>ADBK là hình bình hành
=>AK=DB
mà DB=AC(ABCD là hình chữ nhật)
nên AK=AC
=>ΔAKC cân tại A
b: Xét ΔIAM có IE là phân giác
nên \(\dfrac{ME}{EA}=\dfrac{IM}{IA}\)
mà IA=IK
nên \(\dfrac{ME}{EA}=\dfrac{IM}{IK}\)
Xét ΔIMK có IF là phân giác
nên \(\dfrac{IM}{IK}=\dfrac{MF}{FK}\)
=>\(\dfrac{ME}{EA}=\dfrac{MF}{FK}\)
Xét ΔMAK có \(\dfrac{ME}{EA}=\dfrac{MF}{FK}\)
nên EF//AK
Ta có: EF//AK
AK//BD(AKBD là hình bình hành)
Do đó: EF//BD
Đúng 1
Bình luận (0)
Cho hình chữ nhật ABCD(ABAD), gọi M là trung điểm cạnh AB. Từ M kẻ MN vuông góc với CD tại N( N thuộc CD)a, Trên tia DM lấy điểm K sao cho M là trung điểm của đoạn thẳng DK. Chứng minh tứ giác ADBK là hình bình hành và tam giác AKC cân.b,Gọi I là trung điểm của AK. Tia phân giác của góc AIM cắt AM tại E, tia phân giác của góc KIM cắt MK ở F. Chứng minh EF song song với BD.
Đọc tiếp
Cho hình chữ nhật ABCD(AB>AD), gọi M là trung điểm cạnh AB. Từ M kẻ MN vuông góc với CD tại N( N thuộc CD)
a, Trên tia DM lấy điểm K sao cho M là trung điểm của đoạn thẳng DK. Chứng minh tứ giác ADBK là hình bình hành và tam giác AKC cân.
b,Gọi I là trung điểm của AK. Tia phân giác của góc AIM cắt AM tại E, tia phân giác của góc KIM cắt MK ở F. Chứng minh EF song song với BD.
a.
Xét tứ giác ADBK có: hai đường chéo AB và DK cắt nhau tại trung điểm M của mỗi đường
\(\Rightarrow ADBK\) là hình bình hành
Do ABCD là hình chữ nhật \(\Rightarrow AB\perp BC\Rightarrow AB\) là đường cao tam giác ACK
Theo cmt, ADBK là hbh \(\Rightarrow BK=AD\)
Mà \(AD=BC\) (ABCD là hcn)
\(\Rightarrow BK=BC\Rightarrow AB\) là trung tuyến tam giác ACK
\(\Rightarrow AB\) vừa là đường cao vừa là trung tuyến nên tam giác ACK cân tại A
b.
Do IE là phân giác, áp dụng định lý phân giác trong tam giác IAM:
\(\dfrac{EM}{EA}=\dfrac{IM}{IA}\) (1)
Do IF là phân giác, áp dụng định lý phân giác trong tam giác IMK:
\(\dfrac{FM}{FK}=\dfrac{IM}{IK}\) (2)
Mà I là trung điểm AK \(\Rightarrow IA=IK\) (3)
(1);(2);(3) \(\Rightarrow\dfrac{EM}{EA}=\dfrac{FM}{FK}\Rightarrow EF||AK\) (định lý Talet đảo)
Theo c/m câu a do ADBK là hình bình hành \(\Rightarrow AK||BD\)
\(\Rightarrow EF||BD\)
Đúng 1
Bình luận (0)
Cho hình thang ABCD ( AB // CD; AB < CD). Gọi I là trung điểm của cạnh BD, K là trung điểm của cạnh AC. Từ I kẻ đường thẳng vuông góc với AD, từ K kẻ đường thẳng vuông góc với BC. Chúng cắt nhau tại O. Chứng minh: tam giác ODC cân