Tìm x để (-4x2 + 6x +11) : (x+3) là số nguyên
Những câu hỏi liên quan
Cho S=3/10+3/11+...+3/14
Cm:1<S<2
2,Cho A=6x-5/3x+1
a Tìm x là số nguyên để A nhận giá trị nguyên
b Tim x là số nguyên để A có GTNN
2)\(A=\frac{6x-5}{3x+1}=\frac{6x+2-7}{3x+1}=\frac{2\left(3x+1\right)-7}{3x+1}=2-\frac{7}{3x+1}\)
Do đó, để A nhận giá trị nguyên thì 7 chia hết cho 3x+1 hay (3x+1)EƯ(7)={1;-1;7;-7}
=>3xE{0;-2;6;-8}
=>xE{0;2}
*)Nếu x=0 thì A=2-\(\frac{7}{3\cdot0+1}=2-7=-5\)
*)Nếu x=2 thì A=2-\(\frac{7}{3\cdot2+1}=2-1=1\)
=>Để A có GTNN thì x=0
Vậy để A nhận giá trị nguyên thì xE{0;2}
Để A có GTNN là -5 thì x=0
Đúng 0
Bình luận (0)
Hệ số a thỏa mãn để 4 x 2 - 6 x + a chia hết cho x - 3 là ?
A. a = - 18.
B. a = 8.
C. a = 18.
D. a = - 8.
Ta có phép chia
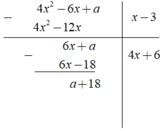
Phép chia trên có số dư là ( a + 18 )
Để 4 x 2 - 6 x + a chia hết cho x - 3 ⇔ a + 18 = 0 ⇔ a = - 18.
Chọn đáp án A.
Đúng 0
Bình luận (0)
x2−3x−4x2−1x2−3x−4x2−1 a) Tìm điều kiện of x để biểu thức A xác địnhb) Rút gọn Ac) Tìm x để A là 1 số nguyên
Đọc tiếp
a) Tìm điều kiện of x để biểu thức A xác định
b) Rút gọn A
c) Tìm x để A là 1 số nguyên
a: ĐKXĐ: x<>1; x<>-1
b: \(A=\dfrac{\left(x-4\right)\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{x-4}{x-1}\)
c: Để A là số nguyên thì x-1-3 chia hết cho x-1
=>\(x-1\in\left\{1;-1;3;-3\right\}\)
=>\(x\in\left\{2;0;4;-2\right\}\)
Đúng 0
Bình luận (0)
Tìm giá trị nguyên của biến x để tại đó giá trị của mỗi biểu thức sau là một số nguyên: 3 x 3 - 4 x 2 + x - 1 x - 4
Ta có:
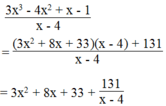
Với x là số nguyên ta có: 3 x 2 + 8 x + 33 là số nguyên.
Để biểu thức đã cho là số nguyên thì 131 ⋮ (x – 4) và x ≠ 4
Suy ra: x – 4 ∈ Ư(131) = {-131; -1; 1; 131}
Ta có: x – 4 = -131 ⇒ x = -127; x – 4 = -1 ⇒ x = 3
x – 4 = 1 ⇒ x = 5; x – 4 = 131 ⇒ x = 135
Vậy với x ∈ {-127; 3; 5; 135} thì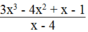 
là số nguyên.
Đúng 0
Bình luận (0)
cho biểu thức √x√x−1+3√x−1−6√x−4x−1−1xx−1+3x−1−6x−4x−1−1
a, rút gon A
b,Tìm x để A = -2
c,Tìm x nguyên để A cũng là số nguyên
tìm x nguyên để 4x+11/6x+5 nguyên
Để 4x+11/6x+5 nguyên thì
4x+11 phải chia hết ch 6x+5
=> 12x+33 phải chia hết cho 6x+5
Mà 12x+10 chia hết cho 6x+5
=>12x+33-12x-10 chia hết cho 6x+5
=>23 chia hết cho 6x+5
=>6x+5 \(\in\)Ư(23)={1;-1;23;-23}
=>x \(\in\){1/2 ; -1; 3;14/3}
mà x nguyên
=> x \(\in\){-1;3}
Đúng 0
Bình luận (0)
Tìm các giá trị nguyên của x để phân thức sau có giá trị là số nguyên:
a) \(A=\dfrac{2x^3-6x^2+x-8}{x-3}\)
Tìm điều kiện của x để giá trị của biểu thức được xác định:a)
3
x
3
(
x
−
1
)
(
x
2
+
2
)
;
b)
−
4...
Đọc tiếp
Tìm điều kiện của x để giá trị của biểu thức được xác định:
a) 3 x 3 ( x − 1 ) ( x 2 + 2 ) ; b) − 4 x 2 25 − 20 x + 4 x 2 ;
c) x 2 − 9 x 2 − 6 x + 9 2 x ; d) x 2 − 9 x 2 + 6 x + 9 x − 3 .
cho C= 6x-1/3x+2 . Tìm x thuộc Z để C có giá trị nguyên và M=5x+11 có giá trị là số chính phương
\(C=\frac{6x-1}{3x+2}=\frac{6x+4-5}{3x+2}=2-\frac{5}{3x+2}\)là số nguyên \(\Leftrightarrow\frac{5}{3x+2}\)nguyên mà \(x\)nguyên nên
\(3x+2\inƯ\left(5\right)=\left\{-5,-1,1,5\right\}\Leftrightarrow x\in\left\{-1,1\right\}\)(vì \(x\)nguyên)
Thử lại thấy \(x=1\)thỏa mãn \(M=5x+11\)là số chính phương.
Vậy giá trị của \(x\)thỏa mãn là \(1\).