Ta có phép chia
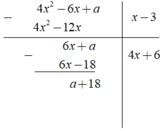
Phép chia trên có số dư là ( a + 18 )
Để 4 x 2 - 6 x + a chia hết cho x - 3 ⇔ a + 18 = 0 ⇔ a = - 18.
Chọn đáp án A.
Ta có phép chia
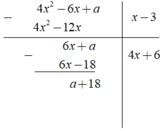
Phép chia trên có số dư là ( a + 18 )
Để 4 x 2 - 6 x + a chia hết cho x - 3 ⇔ a + 18 = 0 ⇔ a = - 18.
Chọn đáp án A.
1)Cho số thực x khác o thỏa mãn x^2 - x - 1=0 . Tính (x^4 - x^8 + 1/x^4 - 1/x^8 - 1)^2019
2) Cho P là số nguyên tố >3. Chứng minh P^2 - 1 chia hết cho 24.
3) Cho a^2 + b^2 + c^2= ab + bc + ca. Chứng minh a=b=c.
1: Cho A=44...4(2.n chữ số 4)
B=22...2(n+1 chữ số 2)
C=88...8(n chữ số 8)
Chứng minh A+B+C+7 là số chính phương
2:Cho m,n \(\in\)Z .Chứng minh 4mn(m2-n2) chia hết cho 24
3:Cho a,b,c\(\in\)Z.Chứng minh
(b-a)(c-a)(d-a)(d-b)(d-c)(c-d) chia hết cho 12
4:Tìm x,y\(\in\)Z . Thỏa mãn x3+y3=1995
Đơn thức 6x^3y^2 chia hết cho đơn thức : A. x^4 B. – 5x^3y C. 2xy^3 D. 3y^4
Giá trị của m để đa thức 𝑥^2 − 2𝑥 + 𝑚 chia hết cho 𝑥 + 2 là: A. 8 B. 0 C. – 8 D. 4
1) Xác định a và b để cho P=x^4+2x^3+ax^2+2x+b là bình phương cuả một đa thức
2) Cho x=a+1. Chứng minh rằng: x^16-a^16=(x^8+a^8)(x^2+a^2)(x+a)
4) Cho a+b+c=0. Chứng minh rằng: 2(a^4+b^4+c^4)=(a^2+b^2+c^2)^2
5) Với giá trị nào của a và b thì đa thức:
f(x)=x^4-3x^3+3x^2+ax+b chia hết cho đa thức g(x)=x^2-3x+4. Tìm đa thức thương.
6) Tìm x ; y ; z trong đẳng thức: x^2+4y^2+9z^2+2x+4y+6z+3=0 (pt)
7) Với a ; b ; c là độ dài 3 cạch của một tam giác. Chứng minh rằng biểu thức M=4b^2c^2-(b^2+c^2-a^2)^2>0
8) Chứng minh rằng (a-b) chia hết cho 6 <=> (a^3+b^3) chia hết cho 6
1)tìm các số tự nhiên n sao cho 19+3n là số chính phương
2)Tìm đa thức bậc 3 P(x) biết P(x) chia cho x-1; x-2; x-3 đều dư 6 và P(-1)=-18
3) Cho a,b,c là các số thực thỏa mãn 1\(\le\)a,b,c\(\le\)3 và a+b+c=6 tìm giá trị lớn nhất của biểu thức: M=a2+b2+c2
Bài 1: Tính nhanh:
37,5.6,5 - 7,5.3,4 - 6,6.7,5 + 3,5.37,5
Bài 2: Tìm x, biết:
a) x^3 - 0,25x = 0
b) x^2 - 10x = - 25
c) x^3 - 13x = 0
d) x^2 + 2x - 1 = 0
Bài 3: CMR: Với mọi n thuộc Z thì:
a) (5n + 2)^2 - 4 chia hết cho 5
b) (n - 3)^2 - (n - 1)^2 chia hết cho 8
c) (n - 6)^2 - (n - 6) chia hết cho 24
Bài 4: Tìm n thuộc N để B = n^2 + 5 là số chính phương
bài 7 : cho biểu thức A=(a^2012+b^2012+c^2012)-(a^2008+b^2008+c^2008) với a,b,c là các số nguyên dương . CM : A chia hết cho 30
bài 8 : Tìm các số thực a,b sao cho đa thức : f(x)=4x^4-11x^3-2ax^2+5bx-6 chia hết hết cho đa thức x^2-2x-3
Bài 1: Phân tích đa thức thành nhân tử : x5+x4+1
Bài 2: Tìm a, b, c, d thỏa mãn điều kiện :
(ax+b)(x2+cx+1)=x3-3x-2
Bài 3: Tìm a,b để x4-3x2+ax+b chia hết cho x2-3x+1
Bài 4: Tìm a để x4-3x3 +2x2-5x+a chia x2-x+1 dư 6
Bài 5: Tính
a) (32+1)(34+1)(38+1)(316+1)
b) x5-15x4+16x3-29x2+13x tại x=14
Bài 6: Cho (a+b)2=2(a2+b2). Chứng minh a=b
Bài 7: Cho a2+b2+c2=ab+ac+bc
Chứng minh a=b=c.
Bài 1: Phân tích đa thức thành nhân tử : x5+x4+1
Bài 2: Tìm a, b, c, d thỏa mãn điều kiện :
(ax+b)(x2+cx+1)=x3-3x-2
Bài 3: Tìm a,b để x4-3x2+ax+b chia hết cho x2-3x+1
Bài 4: Tìm a để x4-3x3 +2x2-5x+a chia x2-x+1 dư 6
Bài 5: Tính
a) (32+1)(34+1)(38+1)(316+1)
b) x5-15x4+16x3-29x2+13x tại x=14
Bài 6: Cho (a+b)2=2(a2+b2). Chứng minh a=b
Bài 7: Cho a2+b2+c2=ab+ac+bc
Chứng minh a=b=c.