a) dễ

b)phương trình hoành độ  giao điểm

a) tự vẽ

b) pt hoành độ

x^2=x+2

giải ra được x1=...;x2=,,,,,

thay x1=...;x2=... vô y=x^2

ta được y1=...;y2=...

ta được A;B có vị trí A(x1;y1);B(x2;y2)

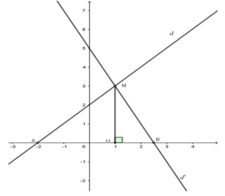
Xét phương trình hoành độ giao điểm của  d 1   v à   d 2

x   +   2   =   − 2 x   +   5 ⇔     x   =   1   ⇒   y   =   3   ⇒   d 1   ∩   d 2   t ạ i   M   ( 1 ;   3 )

Gọi H là chân đường vuông góc kẻ từ M tới Ox. Suy ra MH = 3

d ∩  Ox tại A (−2; 0) ⇒  OA = 2

d’ ∩  Ox tại B 5 2 ; 0   ⇒     O B   =     5 2

  A B   =   O A   +   O B   =   2   + 5 2   =     9 2

SMAB = 1 2  AB.MH = .  1 2 . 3 9 2 =   27 4 (đvdt)

Đáp án cần chọn là: D

a/ Bạn tự vẽ

b/ Ta lập pt hoành độ giao điểm : 

(d1) giao với (d2) : \(-x-5=\frac{1}{4}x\Leftrightarrow x=-4\) thay vào (d1) được y = -1

Vậy A(-4;-1) . Tương tự ta tìm được điểm B(-1;-4)

c/ Ta có : \(AB=\sqrt{\left(x_B-x_A\right)^2+\left(y_B-y_A\right)^2}=\sqrt{\left(-1+4\right)^2+\left(-4+1\right)^2}=3\sqrt{2}\)

\(OA=\sqrt{x_A^2+y_A^2}=\sqrt{4^2+1^2}=\sqrt{17}\) ; \(OB=\sqrt{x_B^2+y_B^2}=\sqrt{1^2+4^2}=\sqrt{17}\) 

=> OAB là tam giác cân

d/ Gọi OH là đường cao hạ từ O xuống AB (H thuộc AB)

Vì tam giác OAB cân tại O nên AH = HB = 1/2AB = \(\frac{3\sqrt{2}}{2}\)

\(OH=\sqrt{OA^2-BH^2}=\sqrt{17-\left(\frac{3\sqrt{2}}{2}\right)^2}=\frac{5\sqrt{2}}{2}\)

\(S_{ABC}=\frac{1}{2}AB.OH=\frac{1}{2}.3\sqrt{2}.\frac{5\sqrt{2}}{2}=\frac{15}{2}\) 

câu b giải pt hoành độ giao điểm bài này de ma

Tọa độ điểm A là:

\(\left\{{}\begin{matrix}y=0\\\left(m-1\right)x-2=0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}y=0\\x\left(m-1\right)=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x=\dfrac{2}{m-1}\end{matrix}\right.\)

=>\(A\left(\dfrac{2}{m-1};0\right)\)

Tọa độ B là:

\(\left\{{}\begin{matrix}x=0\\y=\left(m-1\right)\cdot x-2=0\left(m-1\right)-2=-2\end{matrix}\right.\)

=>B(0;-2)

O(0;0); \(A\left(\dfrac{2}{m-1};0\right)\); B(0;-2)

\(OA=\sqrt{\left(\dfrac{2}{m-1}-0\right)^2+\left(0-0\right)^2}=\sqrt{\left(\dfrac{2}{m-1}\right)^2}=\dfrac{2}{\left|m-1\right|}\)

\(OB=\sqrt{\left(0-0\right)^2+\left(-2-0\right)^2}=\sqrt{0+4}=2\)

Vì Ox\(\perp\)Oy

nên OA\(\perp\)OB

=>ΔOAB vuông tại O

=>\(S_{OAB}=\dfrac{1}{2}\cdot OA\cdot OB=\dfrac{1}{2}\cdot2\cdot\dfrac{2}{\left|m-1\right|}=\dfrac{2}{\left|m-1\right|}\)

Để \(S_{OAB}=8\) thì \(\dfrac{2}{\left|m-1\right|}=8\)

=>\(\left|m-1\right|=\dfrac{1}{4}\)

=>\(\left[{}\begin{matrix}m-1=\dfrac{1}{4}\\m-1=-\dfrac{1}{4}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=\dfrac{5}{4}\\m=\dfrac{3}{4}\end{matrix}\right.\)