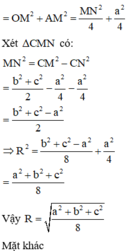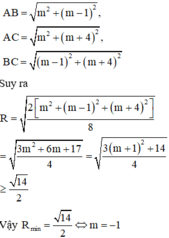Tìm giá trị nhỏ nhất của abcd, biết ab.cd+ab =abcd, và cd.\(\frac{ab}{ba}\)=10

Những câu hỏi liên quan
Cho hình vuông ABCD. Lấy M, N, P, Q lần lượt trên AB, BC, CD, DA. Tìm giá trị nhỏ nhất của chu vi tứ giác MNPQ (M, N, P, Q không là trung điểm của AB, BC, CD, DA)
trả lòi nhanh nhé các bạn nhé
Câu 7:
Giá trị của thỏa mãn là
Câu 8:
Cho hình thang cân ABCD (AB // CD) có AB = 13cm, CD = 25cm, góc .
Diện tích hình thang ABCD bằng
Câu 9:
Ba số có tổng bằng 9 và có tổng các bình phương bằng 53
thì giá trị của biểu thức bằng
Câu 10:
ABCD là hình thang cân có AB//CD, góc , AD = 20cm, AB + CD = 40cm.
Độ dài cạnh CD bằng
Cho hình thang ABCD có diện tích bằng 1 , AB // CD , AC ≥ BD . Tìm giá trị nhỏ nhất của diện tích hình vuông có cạnh bằng cạnh AC
B1: Cho hình thang cân ABCD ( AB // CD; AB < CD ). Biết AC cắt BD tại O và góc DOC = 600. Gọi I, J, K theo thứ tự là trung điểm OD, OA, BC. CM tam giác IJK đều.
B2: Cho x, y thỏa mãn 2x + y = 6.
Tìm giá trị nhỏ nhất của biểu thức A = \(4x^2+y^2\)
B3: Cho x, y thỏa mãn \(x^2+y^2=50.\) Tìm giá trị nhỏ nhất và lớn nhất của biểu thức B = xy
Bài 2. Áp dụng bđt Bunhiacopxki :
\(36=\left(1.\sqrt{4}.x+1.y\right)^2\le\left(1^2+1^2\right)\left(4x^2+y^2\right)\)
\(\Rightarrow4x^2+y^2\ge\frac{36}{2}=18\)
Suy ra Min A = 18 <=> \(\begin{cases}y=2x\\2x+y=6\end{cases}\) \(\Leftrightarrow\begin{cases}x=\frac{3}{2}\\y=3\end{cases}\)
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho tứ diện ABCD với
A
m
;
0
;
0
,
B
0
;
m
-
1
;
0
,
C
0
;
0
;
m
+
4
thỏa mãn
B
C...
Đọc tiếp
Trong không gian Oxyz, cho tứ diện ABCD với A m ; 0 ; 0 , B 0 ; m - 1 ; 0 , C 0 ; 0 ; m + 4 thỏa mãn B C = A D , C A = B D v à A B = C D . Giá trị nhỏ nhất của bán kính mặt cầu ngoại tiếp tứ diện ABCD bằng
A. 7 2
B. 14 2
C. 7
D. 14
Bài 1: Cho tứ giác ABCD có ACp, BDq và M là 1 điểm thay đổi, nằm trong tứ giác. Gọi sMA +MB+MC+MD. Xác định vị trí M để s đạt giá trị nhỏ nhất và tìm giá trị nhỏ nhất đóBài 2: Cho hình thang ABCD có 2 đáy là AB và CD. I là trung điểm của BC và widehat{AID} 90. CM DI là tia phân giác của widehat{D}Bài 3: Cho hình thang ABCD có đáy AB, CD và AD+BCCD. CM các tia phân giác của widehat{A} và widehat{B} cắt nhau tại 1 điểm thuộc cạnh CD
Đọc tiếp
Bài 1: Cho tứ giác ABCD có AC=p, BD=q và M là 1 điểm thay đổi, nằm trong tứ giác. Gọi s=MA +MB+MC+MD. Xác định vị trí M để s đạt giá trị nhỏ nhất và tìm giá trị nhỏ nhất đó
Bài 2: Cho hình thang ABCD có 2 đáy là AB và CD. I là trung điểm của BC và \(\widehat{AID}\)= 90. CM DI là tia phân giác của \(\widehat{D}\)
Bài 3: Cho hình thang ABCD có đáy AB, CD và AD+BC=CD. CM các tia phân giác của \(\widehat{A}\) và \(\widehat{B}\) cắt nhau tại 1 điểm thuộc cạnh CD
Cho hình chữ nhật ABCD. M, N, P, Q là các điểm thuộc AB, BC, CD, DA. Tìm giá trị nhỏ nhất của chu vi tứ giác MNPQ. Khi đó tứ giác MNPQ là hình gì
Gọi I, H, K lần lượt là trung điểm các đoạn QM, QN, PN.
Xét tam giác AQM vuông tại A có AI là đường trung tuyến nên suy ra AI=12QMAI=12QM
IH là đường trung bình của tam giác QMN nên IH=12MNIH=12MN, IH // MN.
Tương tự KC=12NP,HK=12PQKC=12NP,HK=12PQ, HK // PQ.Do đó AI+IH+HK+KC=12PMNPQAI+IH+HK+KC=12PMNPQ
Mặt khác nếu xét các điểm A, I, H, K, C ta có: AI+IH+HK+KC≥ACAI+IH+HK+KC≥ACDo đó PMNPQ≥2ACPMNPQ≥2AC (không đổi)
Dấu “=” xảy ra khi và chỉ khi A, I, H, K, C thẳng hàng theo thứ tự đó.
Điều đó tương đương với MN//AC//QP, QM//BD//NP hay MNPQ là hình bình hành.
Vậy giá trị nhỏ nhất của chu vi MNPQ là 2AC.
Cho hình chữ nhật ABCD. M, N, P, Q là các điểm thuộc AB, BC, CD, DA. Tìm giá trị nhỏ nhất của chu vi tứ giác MNPQ. Khi đó tứ giác MNPQ là hình gì?
Cho hình chữ nhật ABCD. M, N, P, Q là các điểm thuộc AB, BC, CD, DA. Tìm giá trị nhỏ nhất của chu vi tứ giác MNPQ. Khi đó tứ giác MNPQ là hình gì? Vì sao
Gợi ý thôi nhé. gọi E,F lần lượt là trung điểm MN, PQ.
1. So sánh MN với BE, PQ với DF
2. So sánh MQ + NP với EF (gợi ý: áp dụng Thales)
3. So sánh BE + EF + DF với BD
4. Kết luận (cẩn thận khi trả lời tứ giác BDEF là hình gì)
Hiểu ko ku, nếu hiểu giải thích t cái, tìm gt nhỏ nhất của tg MNPQ đó, ko hiểu
Đúng 0
Bình luận (0)