Tính biệt thức ∆ của phương trình : 5x^2+x-4=0 :
A,81
B,-79
C,21
D,-19
Những câu hỏi liên quan
Xác định các hệ số a, b, c ; tính biệt thức ∆ rồi tìm nghiệm của các phương trình : 2 x 2 – 5x + 1 = 0
Phương trình 2 x 2 – 5x + 1 = 0 có a = 2, b = -5, c = 1
Ta có: ∆ = b 2 – 4ac = - 5 2 – 4.2.1 = 25 – 8 = 17 > 0
∆ = 17
Phương trình có 2 nghiệm phân biệt :
Đúng 0
Bình luận (0)
6. Biết rằng phương trình x 3 −3x 2 +3 0 có ba nghiệm phân biệt. Chứng minh rằng trong ba nghiệm này có hai nghiệm a,b thoả mãn ab+3 a+2b.7. Cho đa thức P(x) 2x 4 −x 3 −5x 2 +5x−5. Gọi a,b, c là ba nghiệm phân biệt của đa thức Q(x) x 3 −3x+1. Tính P(a).P(b).P(c).8. Biết rằng phương trình P(x) x 3 +3x 2 −1 có ba nghiệm phân biệt a b c. Chứng minh rằng c a 2 +2a− 2,b c 2 +2c−2,a b 2 +2b−2.
Đọc tiếp
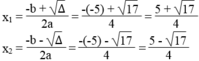
6. Biết rằng phương trình x 3 −3x 2 +3 = 0 có ba nghiệm phân biệt. Chứng minh rằng trong ba nghiệm này có hai nghiệm a,b thoả mãn ab+3 = a+2b.
7. Cho đa thức P(x) = 2x 4 −x 3 −5x 2 +5x−5. Gọi a,b, c là ba nghiệm phân biệt của đa thức Q(x) = x 3 −3x+1. Tính P(a).P(b).P(c).
8. Biết rằng phương trình P(x) = x 3 +3x 2 −1 có ba nghiệm phân biệt a < b < c. Chứng minh rằng c = a 2 +2a− 2,b = c 2 +2c−2,a = b 2 +2b−2.
Cho phương trình x2-5x+6=0
a) Tính biệt số đentatê. Rồi cho biết số nghiệm của phương trình
b) Tính tổng và tích hai nghiệm của phương trình trên
Cho phương trình 2x ^ 2 - 5x - 3 = 0 Chứng minh phương trình luôn có 2 nghiệm phân biệt x_{1}, x_{2} . Không giải phương trình, hãy tính giá trị biểu thức A = 2x_{1} - x_{1} ^ 2 + 2x_{2} - x_{2} ^ 2
bạn viết lại bth nhé
\(\Delta=25-4\left(-3\right).2=25+24=49>0\)
Vậy pt luôn có 2 nghiệm pb
Đúng 1
Bình luận (0)
Cho phương trình x2 + 5x − 4 = 0 . Gọi 1 2 x ; x là hai nghiệm của phương trình. Không
giải phương trinh, hăy tính giá trị biểu thức 2 2
1 2 1 2 Q = x + x + 6x x .
b) Gọi x_{1} x_{2}! là hai nghiệm dương của phương trình : x ^ 2 - 5x + 4 = 0 Không giải phương trình hãy tính giá trị biểu thức: A = √x_{1}/x_{2} - √x_{2}/x_{1}
\(A^2=\dfrac{x_1}{x_2}+\dfrac{x_2}{x_1}-2\cdot\sqrt{\dfrac{x_1}{x_2}\cdot\dfrac{x_2}{x_1}}\)
\(=\dfrac{x_1^2+x_2^2}{x_1x_2}-2\)
\(=\dfrac{\left(-5\right)^2-2\cdot4}{4}-2=\dfrac{25-8-8}{2}=\dfrac{9}{2}\)
=>A=3/căn 2
Đúng 1
Bình luận (0)
18 tháng 4 2022 lúc 19:24
Cho phương trình: \(x^4-5x^2+m=0\)
Tìm \(m\) để phương trình có 4 nghiệm phân biệt.
Đặt \(x^2=a\left(a\ge0\right)\)khi đó phương trình tương đương với
\(a^2-5a+m=0\)(*)
Để phương trình có 4 nghiệm phân biệt thì phương trình (*) phải có 2 nghiệm phân biệt dương
\(< =>\left\{{}\begin{matrix}\Delta>0\\x_1.x_2>0\\x_1+x_2>0\end{matrix}\right.< =>\left\{{}\begin{matrix}25-4m>0\\m>0\\5>0\end{matrix}\right.\)
\(< =>\dfrac{25}{4}>m>0\)
Đúng 1
Bình luận (2)
cho phương trình : \(x^2-x-1=0\) có hai nghiệm phân biệt \(x_1,x_2\) không giải phương trình hãy tính giá trị của biểu thức T = \(x_1^4-x_1^2+x_2^2-x_1\)
Cho phương trình \(x^2-5x-m-4=0\)( x là ẩn số, m là tham số). Tìm m để phương trình có 2 nghiệm phân biệt \(x_1x_2\) thỏa \(x^2_1+x_2^2+x_1x_2=19\)
Để pt có 2 nghiệm phân biệt x1;x2 thì \(\Delta=\left(-5\right)^2-4\left(-m-4\right)=41+4m>0\Leftrightarrow m>\frac{-41}{4}\)
Với m>-41/4 thì theo hệ thức Vi-et: \(\hept{\begin{cases}x_1+x_2=5\\x_1x_2=-m-4\end{cases}}\)
\(x_1^2+x_2^2+x_1x_2=19\Leftrightarrow\left(x_1+x_2\right)^2-x_1x_2=19\Leftrightarrow5^2-\left(-m-4\right)=19\)<=>m=-10(tm m>-41/4)
Vậy...
Đúng 0
Bình luận (0)