1.thước đo góc có cấu tạo như thế nào???
2.Thế nào là:Tia nằm giữa hai tia?Điểm nằm trong góc?
1,Thế nào là nửa mặt phẳng?
2,Thế nào là góc?
3,Thước đo góc có cấu tạo như thế nào?
Nửa mặt phẳng là một phần của mặt phẳng bị chia ra bởi một đường thẳng, hai nửa mặt phẳng chung bờ được gọi là hai nửa mặt phẳng đối nhau.
Trong hình học phẳng, Góc nằm giữa hai đường thẳng cắt nhau tại một điểm. Hai đường thẳng được gọi là cạnh của góc. Giao điểm của chúng gọi là đỉnh của góc. Khi hai đường thẳng song song với nhau, không cắt nhau tại điểm nào (hoặc cũng có thể hiểu là cắt nhau tại vô cực), góc giữa chúng bằng không và không có đỉnh xác định (hoặc đỉnh ở vô cực).
Nếu lấy một vòng tròn đơn vị có tâm tại giao điểm O của hai đường thẳng và hai đường thẳng cắt vòng tròn đơn vị tại A1, A2 và B1, B2. Góc giữa hai đường thẳng sẽ là độ dài cung nối giữa Ai và Bj, với i và j bằng 1 hoặc 2 tùy theo quy ước, chia cho đơn vị độ dài để loại bỏ thứ nguyên và nhân với hằng số tỷ lệ tùy thuộc vào đơn vị đo góc[cần dẫn nguồn].
Trong không gian ba chiều, góc giữa hai mặt phẳng (còn được gọi là góc khối) là phần không gian giới hạn bởi hai mặt phẳng đó, được đo bằng góc giữa hai đường thẳng trên hai mặt phẳng cùng trực giao với giao tuyến của hai mặt phẳng.
Khái niệm góc cũng được mở rộng cho đại số tuyến tính. Để loại bỏ rắc rối trong quy ước tính góc, có thể thay các đường thẳng bằng các véctơ thể hiện không chỉ độ nghiêng mà còn cả hướng. Khi tịnh tiến các véctơ về cùng tâm O và lấy một vòng tròn đơn vị tại tâm này, các véctơ sẽ chỉ cắt vòng tròn này tại hai điểm A và B. Độ lớn góc giữa hai véctơ sẽ là độ dài cung trên vòng trò

Thước đo góc (180 độ).

Thước đo góc (360 độ)

A 400g thước dùng đơn vị grads.

một thước đo độ đôi "Cras Navigation Plotter".

Thước đo góc nửa tròn(180 độ).
n nối A và B chia cho đơn vị độ dài.
Thước đo góc hay còn gọi là thước đo độ là một dụng cụ hình tròn, bán nguyệt hoặc vuông thường làm bằng nhựa dẻo trong suốt dùng đo góc. Hầu hết các thước đo góc dùng đơn vị độ (°).
Thước đo góc ứng dụng nhiều trong cơ khí là kỹ thuật nhưng đặc biệt thường xuyên sử dụng trong trường học.
Thước đo góc thường phẳng, tuy nhiên một số loại công phu có thêm hai cần xoay giúp đo góc chính xác hơn
1. Nửa mặt phẳng bờ a là hình gồm đường thẳng a và 1 phần mặt phẳng được chia ra bởi a.
2. Góc là hình gồm 2 tia chung gốc.
3. Thước đo góc là một nửa hình tròn được chia thành 180 phần bằng nhau và được ghi từ 0 (độ) đến 180 (độ). Ta gọi tâm của nửa hình tròn này là tâm của thước.
^^ nha^^
Thế nào là tia năm giữa hai tia ,thế nào là điểm nằm trong góc
nhanh thì tick
Vẽ góc xOy. Vẽ tia Oz nằm giữa hai tia Ox,Oy. Làm thế nào để chỉ đo 2 lần mà biết được số đo của ba góc xOy, yOz,xOz. Có mấy cách làm ?
BÀI ÔN HÌNH HỌC
1. Trả lời câu hỏi sau
a) Thế nào là nửa mặt phẳng ?
b) thế nào là góc ?
c) Thế nào là: Góc bẹt ? Góc vuông ? Góc nhọn ? Góc tù ?
d) Thế nào là: Tia nằm giữa 2 tia ? Điểm nằm trong góc ?
e) Đường tròn là gì ? Hình tròn là gì ?
f) Thế nào là: Cung ? Dây cung ? Đường kính của đường tròn ?
g) Tam giác là hình như thế nào ?
h) Vẽ tam giác biết độ dài 3 cạnh bằng cách sử dụng compa ta làm như thế nào ?
Hình gồm đường thẳng và 1 phần mặt phẳng bị chia ra bởi đường thẳng được gọi là một nửa mặt phẳng
Góc là hình gồm hai tia chung góc
Góc nhọn có thể được tạo thành từ 2 đường thẳng có chung 1 giao điểm trong mặt phẳng, hoặc trong tam giác bất kỳ. Góc nhọn là góc có giá trị nhỏ hơn 90°. Giá trị của góc nhọn nằm trong khoảng > 0 và < 90°.
Góc tù cũng được tạo thành từ 2 đường thẳng trong mặt phẳng, góc tù có giá trị lớn hơn góc vuông và nhỏ hơn tổng 3 góc trong tam giác.
Góc bẹt là góc có giá trị bằng 180°, nữa đường tròn là có giá trị bằng góc bẹt.
Góc vuông là loại góc có giá trị bằng 90°.
Đường tròn tâm O, bán kính R là hình gồm các điểm cách O một khoảng bằng R, kí hiệu (O; R )
Hình tròn là hình gồm các điểm nằm trên đường tròn và các điểm nằm bên trong đường tròn đó
Vẽ góc xOy. Vẽ tia Oz nằm giữa hai tia Ox, Oy. Làm thế nào để chỉ đo hai lần mà biết được số đo của cả ba góc xOy, yOz, xOz. Có mấy cách làm?
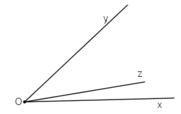
Cách 1: Đo hai góc xOz và yOz. Tổng số do hai góc này chính là số đo của góc xOy.
Cách 2: Đo góc xOy và góc xOz (hoặc góc yOz). Hiệu số đo hai góc này chính là góc đo của góc yOz (hoặc xOz).
Vẽ góc xOy. Vẽ tia Oz nằm giữa hai tia Ox, Oy. Làm thế nào để chi đo hai lần mà biết được số đo của ba góc xOy, yOz, xOz. Có mấy cách ?
Cách 1: Đo hai góc xOz và yOz. Tổng số do hai góc này chính là số đo của góc xOy.
Cách 2: Đo góc xOy và góc xOz (hoặc góc yOz). Hiệu số đo hai góc này chính là góc đo của góc yOz (hoặc xOz).
Cách 3: Gọi Oz' là tia đối của tia Oz. Ta có: yOz + yOz' = 180o ; xOz + xOz' = 180o
Do đó: đo hai góc yOz' và xOz' ta suy ra được số đo hai góc yOz và xOz. Tổng số đo của hai góc yOz và xOz là số đo của góc xOy.

Có hai cách làm:
1) Đo hai góc xOz và yOz. Tổng hai số đo này là số đo của hai góc xOy.
2) Đo góc xOy và một trong hai góc xOz, yOz. Tính hiệu hai số đo này được số đo của góc còn lại.
Gọi Oz' là tia đối của tia Oz. Ta có: góc yOz + góc yOz' = 180o ; góc xOz + góc xOz' = 180o
Do đó: đo hai góc yOz' và xOz' ta suy ra được số đo hai góc yOz và xOz. Tổng số đo của hai góc yOz và xOz là số đo của góc xOy.

Có hai cách làm:
1) Đo hai góc xOz và yOz. Tổng hai số đo này là số đo của hai góc xOy.
2) Đo góc xOy và một trong hai góc xOz, yOz. Tính hiệu hai số đo này được số đo của góc còn lại.
Gọi Oz' là tia đối của tia Oz. Ta có: góc yOz + góc yOz' = 180o ; góc xOz + góc xOz' = 180o
Do đó: đo hai góc yOz' và xOz' ta suy ra được số đo hai góc yOz và xOz. Tổng số đo của hai góc yOz và xOz là số đo của góc xOy.
Vẽ góc xOy.Vẽ tia Oz nằm giữa 2 tia Ox,Oy.Làm thế nào chỉ đo hai lần mà biết được số đo của 3 góc xOy,yOz,xOz.Có mấy cách làm?
Vẽ góc xOy. Vẽ tia Oz nằm giữa hai tia Ox, Oy. Làm thế nào để chỉ đo hai lần mà biết được số đo của cả ba góc xOy, yOz, xOz. Có mấy cách làm?
Giải

Cách 1: Đo hai góc xOz và yOz. Tổng số do hai góc này chính là số đo của góc xOy
Cách 2: Đo góc xOy và góc xOz (Hoặc góc yOz) Hiệu số đo hai góc này chính là góc đo của góc yOz (hoặc xOz)
Cách 3: Gọi Oz’ là tia đối của tia Oz. Ta có: yOz + yOz’ = 1800 ; xOz + xOz’ = 1800
Do đó: đo hai góc yOz’ và xOz’ ta suy ra được số đo hai góc yOz và xOz. Tổng số đo của hai góc yOz và xOz là số đo của góc xOy.
Không dùng thước đo góc, làm thế nào để biết số đo góc đó.
Ban Hoài vẽ góc xOy và đó bạn Đông làm thế nào có thể biết được số đo của góc này khi không có thước đo góc. Bạn Đông làm như sau:
- Chọn các điểm A, B lần lượt thuộc các tia Ox và Oy sao cho OA = OB = 2 cm.
- Đo độ dài đoạn thẳng AB được AB = 3,1 cm.
Từ các dữ kiện trên bạn Đông tính được \(\cos \widehat {xOy}\) từ đó suy ra độ lớn góc xOy.
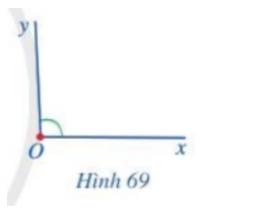
Em hãy cho biết số đo góc xOy ở Hình 69 bằng bao nhiêu độ (làm tròn kết quả đến hàng đơn vị).
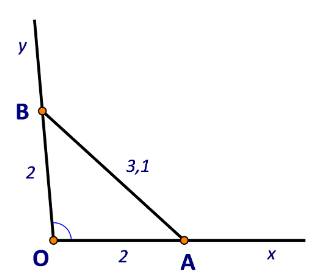
Áp dụng định lí cosin trong tam giác OAB, ta có:
\(\begin{array}{l}\cos O = \frac{{O{A^2} + O{B^2} - A{B^2}}}{{2.OA.OB}} = \frac{{{2^2} + {2^2} - 3,{1^2}}}{{2.2.2}} \approx - 0,2\\ \Rightarrow \widehat {xOy} \approx {102^o}\end{array}\)