(-2x2yz).(-3xy3z) = [(-2).(-3)].(x2.x)(y.y3).(z.z) = 6.x3.y4.z2

Đơn thức trên có hệ số bằng 6.

Bậc của tích trên là tổng bậc của các biến :

Biến x có bậc 3

Biến y có bậc 4

Biến z có bậc 2

⇒ Tích có bậc : 3 + 4 + 2 = 9

a, Tích hai đơn thức : -0,5 \(x^2\)\(y\)z và -3\(xy^3z\) 

    A = -0,5 \(x^2\)yz \(\times\) ( -3\(xy^3\)z)

    A = 1,5\(x^3\)y⁴z²

b, bậc của đa thức là: 3 + 4 + 2 = 9

Hệ số cao nhất là 1,5

Chương trình Toán 7 mới hiện nay chỉ học đơn thức 1 biến, không còn học đơn thức nhiều biến như cũ nữa

Ta có:  2 x 2 y z + 5 x y 2 z − 5 x 2 y z + x y 2 z + x y z

= 2 x 2 y z − 5 x 2 y z + 5 x y 2 z + x y 2 z + x y z

= − 3 x 2 y z + 6 x y 2 z + x y z

Đa thức  − 3 x 2 y z + 6 x y 2 z + x y z có bậc là 2 + 1 + 1  = 4

Chọn đáp án B

Ta có

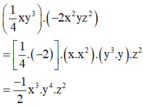
Đơn thức trên có hệ số bằng -1/2.

Bậc của tích trên là tổng bậc của các biến :

Biến x có bậc 3

Biến y có bậc 4

Biến z có bậc 2

⇒ Tích có bậc : 3 + 4 + 2 = 9.

Bạn vui lòng viết dưới dạng công thức trực quan để mn có thể giúp đỡ bạn tốt nhất nhé!!!

P/s: Nếu ko biết viết dưới dạng công thức trực quan thì ib mình!

a) 2x²yz . (-3xy³z)²

= 2x²yz . 9x²y⁶z²

= (2.9) . (x²x²) . (yy⁶) . (z.z²)

= 18x⁴y⁷z³

=> Bậc là 7

b) \(\left(-12xyz\right)\left(-\frac{4}{3}x^2yz^3\right)^3y\)

\(=-12xyz\left(-\frac{4}{3}\right)^3x^6y^3z^9y\)

\(=-12xyz\frac{-64}{27}x^6y^3z^9y\)

\(=\left[\left(-12\right)\left(-\frac{64}{27}\right)\right]\left(xx^6\right)\left(yy^3y\right)\left(zz^9\right)\)

\(=\frac{259}{6}x^7y^5z^{10}\)

=> Bậc 10

c) \(5x\left(-2xy^2\right)\left(3xyz^3\right)\)

\(=5x\left(-2\right)xy^23xyz^3\)

\(=\left[5.\left(-2\right).3\right]\left(xxx\right)\left(y^2y\right)z^3\)

\(=-30x^3y^3z^3\)

=> Bậc 3

d) \(\left(-x^2y^3\right)^2x^2yz\)

\(=-x^4y^6x^2yz\)

\(=\left(-1\right)\left(x^4x^2\right)\left(y^6y\right)z\)

\(=\left(-1\right)x^6y^7z\)

\(=-x^6y^7z\)

=> Bậc 7

Tích của đơn thức : -1/2x^3y^4z^2
Bậc : 4
hệ số: -1/2

B

A

1. 

Tại x = -1, có : 

2.(-1)² - 5.(-1) + 2 

= 2.1 + 5 + 2 

= 9 

Tại x = \(\dfrac{1}{2}\), có : 

\(2.\left(\dfrac{1}{2}\right)^2-5.\dfrac{1}{2}+2\)

= \(2.\dfrac{1}{4}-2,5+2\)

= 0,5 - 2,5 + 2

= 0

2. 

\(\dfrac{1}{2}xy^2.\left(-3xyz\right).2x^2z\)

= -3x⁴y³z²

- Hệ số : -3

- Bậc : 9

thay x =-1 vào bt ta được

\(2\left(-1\right)^2-5\left(-1\right)+2=2+5+2=9\)

thay x=1/2 vào bt ta được 

\(2.\left(\dfrac{1}{2}\right)^2-5.\dfrac{1}{2}+2=\dfrac{1}{2}-\dfrac{5}{2}+\dfrac{4}{2}=0\)

\(\dfrac{1}{2}xy^2.-3xyz.2x^2z=-3x^4y^3z\)²

hệ số là -3 bậc 9

`@` `\text {Ans}`

`\downarrow`

`-0,5x^2yz*(-3xy^3z)`

`= [(-0,5)*(-3)]*(x^2*x)*(y*y^3)*(z*z)`

`= 1,5x^3y^4z^2`

Hệ số: `1,5`

Bậc: `3+4+2 = 9`

`@` `\text {Kaizuu lv u}`