diện tích lục giác đều cạnh là 3cm

Những câu hỏi liên quan
Tính diện tích lục giác đều có độ dài cạnh là 3cm ...
Area = \(\left(3\sqrt{3}.s^2\right):2,s=3\)
= \(\left(3\sqrt{3}.3^2\right):2\)
= \(\left(3\sqrt{3}.9\right):2\)
= \(\left(27\sqrt{3}\right):2\)
= 23,3826859...
K mình nha
Chúc bạn học tốt
Đúng 0
Bình luận (0)
Diện tích lục giác đều có độ dài cạnh 3cm bằng bao nhiêu cm2.
Diện h hình lục giác là ;
.............................................=..............( cm2)
Đáp số : ..........................
T I C K mk cái nha
Đúng 0
Bình luận (0)
ta có ct tính lục giác đều
(3√3 s2)/ 2
thay vào mà tính
Đúng 0
Bình luận (0)
Cho hình lục giác đều ABCDEF có diện tích là 2022 dm2. Nối các điểm giữa của các cạnh của hình lục giác đều đó lại được một hình lục giác đều mới. Tính điện tích hình đó.
vẽ một lục giác đều abcdef có độ dài cạnh đáy 6 cm a, tính diện tích tam giác ABC
b,Tứ giác ACDF là hình gì? Tính diện tích tứ giác ACDF
c,Tính diện tích lục giác ABCDEF
tính diện tích hình lục giác đều biết cạnh là 10 cm
Diện tích hình lục giác đều cạnh 10cm là:
\(S=\dfrac{3\sqrt{3}}{2}\cdot10^2=3\sqrt{3}\cdot50=150\sqrt{3}\left(cm^2\right)\)
Đúng 0
Bình luận (0)
Cho ABCDEF là một hình lục giác đều (có sáu cạnh bằng nhau, sáu góc bằng nhau). Điểm G nằm trên cạnh AF sao cho GF = 2/5AF. Biết diện tích của hình lục giác bằng 60 cm2 , tính diện tích phần tô đậm.
Tính diện tích xung quanh , diện tích toàn phần và thể tích của lăng trụ đứng có chiều cao h và cạnh đáy lần lượt là: a)hình vuông cạnh a b)Tam giác đều cạnh a c) lục giác đều cạnh a d) hình thang cân,đáy lớn là 2a,các cạnh còn lại a e) hình thoi có 2 đường chéo là 6a và 8a
Tính diện tích xung quanh, diện tích toàn phần và thể tích của lăng trụ đứng có chiều cao h và đáy lần lượt là:
a) Hình vuông cạnh a;
b) Tam giác đều cạnh a;
c) Lục giác đều cạnh a;
d) Hình thang cân, đáy lớn là 2a, các cạnh còn lại bằng a;
e) Hình thoi có hai đường chéo là 6a và 8a.
Gọi h là chiều cao của hình lăng trụ đứng.

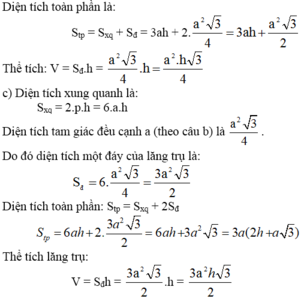


Đúng 0
Bình luận (0)
TÍNH DIỆN TÍCH HÌNH TAM GIÁC ĐỀU
CÒ ĐỘ DÀI 3 CẠNH LÀ 3cm
Hình:
Kẻ đường cao AH( H thuộc BC)
Vì tam giác vuông ACH có góc C bằng 60 độ nên tam giác vuông ACH là nửa tam giác đều
Suy ra:
\(CH=\frac{1}{2}AC=\frac{1}{2}\cdot3=1,5\)
Áp dụng Pytago vào tam giác vuông ACH đề tìm AH:
Ta có: \(AC^2=CH^2+AH^2\)
\(AH^2=AC^2-CH^2=9-2,25=6,75\)
Suy ra: \(AH=\sqrt{6,75}\)
Vậy \(S_{\Delta ABCD}=\frac{\sqrt{6,75}\cdot3}{2}=\frac{9\sqrt{3}}{4}\)
Từ đây người ta hình thành công thức tính diện tích tam giác đều có độ dài ba cạnh là a
Ta có: \(S=a^2\cdot\frac{\sqrt{3}}{4}\)(áp dụng định lí Heron để suy ra)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời




















