trên mặt phẳng tọa độ cho điểm A(8;9). Hoành độ là

Những câu hỏi liên quan
Câu 8: Trên mặt phẳng tọa độ Oxy, cho điểm A(-3; 1); B(5; 5). Khoảng cách giữa A và B là:
\(AB=\sqrt{\left(5-\left(-3\right)\right)^2+\left(5-1\right)^2}=\sqrt{8^2+4^2}=4\sqrt{5}\)
Đúng 0
Bình luận (0)
Trong không gian tọa độ Oxyz, cho điểm A(3;-2;5). Hình chiếu vuông góc của điểm A trên mặt phẳng tọa độ (Oxz)
Đọc tiếp
Trong không gian tọa độ Oxyz, cho điểm A(3;-2;5). Hình chiếu vuông góc của điểm A trên mặt phẳng tọa độ (Oxz)
![]()
![]()
![]()
![]()
Trên mặt phẳng tọa độ xOy, cho đường thẳng (d): y = x-3 và parabol (P) : y= -2x2.
a) Vẽ (d) trên cùng một mặt phẳng tọa độ xOy
b) Tìm tọa độ của giao điểm M và N của (d) và (P)
c) Tính diện tích tam giác OMN với O là gốc tọa độ
b) Phương trình hoành độ giao điểm là:
\(-2x^2=x-3\)
\(\Leftrightarrow-2x^2-x+3=0\)
\(\Leftrightarrow-2x^2+2x-3x+3=0\)
\(\Leftrightarrow-2x\left(x-1\right)-3\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(-2x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\-2x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\-2x=3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-\dfrac{3}{2}\end{matrix}\right.\)
Thay x=1 vào hàm số y=x-3, ta được:
y=1-3=-2
Thay \(x=-\dfrac{3}{2}\) vào hàm số y=x-3, ta được:
\(x=-\dfrac{3}{2}-3=-\dfrac{9}{2}\)
Vậy: M(1;-2) và \(N\left(-\dfrac{3}{2};-\dfrac{9}{2}\right)\)
Đúng 1
Bình luận (0)
Cho số phức z thỏa mãn
3
-
4
i
z
-
4
z
8
. Trên mặt phẳng tọa độ, khoảng cách từ gốc tọa độ đến điểm biểu diễn số phức z thuộc tập nào? A.
9
4
;
+
∞
B.
1...
Đọc tiếp
Cho số phức z thỏa mãn 3 - 4 i z - 4 z = 8 . Trên mặt phẳng tọa độ, khoảng cách từ gốc tọa độ đến điểm biểu diễn số phức z thuộc tập nào?
A. 9 4 ; + ∞
B. 1 4 ; 5 4
C. 0 ; 1 4
D. 1 2 ; 9 4
Đáp án D
Ta có 3 - 4 i z - 4 z = 8 ⇔ 3 - 4 i z = 8 + 4 z ( * )
Lấy môđun hai vế của (*) và sử dụng công thức z 1 z 2 = z 1 . z 2 , ta được
* ⇔ 3 - 4 i z = 8 + 4 z ⇔ 3 - 4 i . z = 4 2 + 1 z ⇔ 5 z = 4 2 + 1 z
⇔ 5 z 2 = 4 2 z + 1 ⇔ 5 z 2 - 8 z - 4 = 0 ⇔ z = 2
Gọi M(x;y) là điểm biểu diễn số phức z. Khi đó O M = x 2 + y 2 = z = 2 ∈ 1 2 ; 9 4 .
Đúng 0
Bình luận (0)
Trên mặt phẳng tọa độ cho 2 điểm A(-3;4);B(4;2). Tìm Tọa Độ Của Điểm C để Tam Giác ABC Đều
Cho số phức z thỏa mãn (3-4i)z -
4
z
8. Trên mặt phẳng tọa độ, khoảng cách từ gốc tọa độ đến điểm biểu diễn số phức z thuộc tập nào?
A
.
(
9
4
;
+
∞
)
B
.
(
1
4
;
5
4
)
C
.
(...
Đọc tiếp
Cho số phức z thỏa mãn (3-4i)z - 4 z = 8. Trên mặt phẳng tọa độ, khoảng cách từ gốc tọa độ đến điểm biểu diễn số phức z thuộc tập nào?
A . ( 9 4 ; + ∞ )
B . ( 1 4 ; 5 4 )
C . ( 0 ; 1 4 )
D . ( 1 2 ; 9 4 )
Đáp án D
Ta có (3-4i)z -
4
z
= 8 ![]()
Lấy môđun hai vế của (*) và sử dụng công thức ![]() ta được
ta được
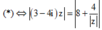
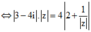
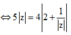
![]()
![]()
Gọi M(x;y) là điểm biểu diễn số phức z. Khi đó OM = 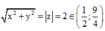
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz cho hai điểm
A
0
;
0
;
3
,
B
−
2
;
0
;
1
và mặt phẳng
α
:
2
x
−
y
+
2
z
+
8...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz cho hai điểm A 0 ; 0 ; 3 , B − 2 ; 0 ; 1 và mặt phẳng α : 2 x − y + 2 z + 8 = 0 . Hỏi có bao nhiêu điểm C trên mặt phẳng α sao cho tam giác ABC đều.
A. 2
B. 0
C. 1
D. Vô số
Cho số phức z thỏa mãn (3-4i)z -
4
|
z
|
8. Trên mặt phẳng tọa độ, khoảng cách từ gốc tọa độ đến điểm biểu diễn số phức z thuộc tập nào?
A
.
9
4
;
+
∞
B
.
1
4...
Đọc tiếp
Cho số phức z thỏa mãn (3-4i)z - 4 | z | = 8. Trên mặt phẳng tọa độ, khoảng cách từ gốc tọa độ đến điểm biểu diễn số phức z thuộc tập nào?
A . 9 4 ; + ∞
B . 1 4 ; 5 4
C . 0 ; 1 4
D . 1 2 ; 9 4
Đáp án D
Ta có 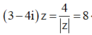
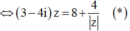
Lấy môđun hai vế của (*) và sử dụng công thức ![]() ta được
ta được
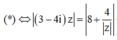

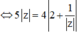
![]()
![]()
Gọi M(x;y) là điểm biểu diễn số phức z. Khi đó
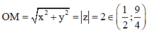
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho điểm
M
1
;
−
2
;
3
. Tọa độ điểm A là hình chiếu vuông góc của điểm M trên mặt phẳng
O
y
z
là A.
A
0
;
−
2
;
3...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm M 1 ; − 2 ; 3 . Tọa độ điểm A là hình chiếu vuông góc của điểm M trên mặt phẳng O y z là
A. A 0 ; − 2 ; 3
B. A 1 ; 0 ; 3
C. A 1 ; − 2 ; 3
D. A 1 ; − 2 ; 0
Đáp án A
Ta có
x A = 0 y A = y M = − 2 z A = z M = 3 ⇒ A 0 ; − 2 ; 3
Đúng 0
Bình luận (0)















