Đáp án D
Ta có (3-4i)z -
4
z
= 8 ![]()
Lấy môđun hai vế của (*) và sử dụng công thức ![]() ta được
ta được
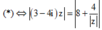
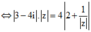
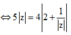
![]()
![]()
Gọi M(x;y) là điểm biểu diễn số phức z. Khi đó OM = 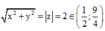
Đáp án D
Ta có (3-4i)z -
4
z
= 8 ![]()
Lấy môđun hai vế của (*) và sử dụng công thức ![]() ta được
ta được
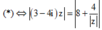
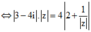
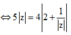
![]()
![]()
Gọi M(x;y) là điểm biểu diễn số phức z. Khi đó OM = 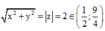
Cho số phức z thỏa mãn (3-4i)z - 4 | z | = 8. Trên mặt phẳng tọa độ, khoảng cách từ gốc tọa độ đến điểm biểu diễn số phức z thuộc tập nào?
A . 9 4 ; + ∞
B . 1 4 ; 5 4
C . 0 ; 1 4
D . 1 2 ; 9 4
Cho số phức z thỏa mãn iz + 2 - i = 0. Khoảng cách từ điểm biểu diễn của z trên mặt phẳng tọa độ Oxy đến điểm M(3;-4) là:
A. 2 5
B. 13
C. 2 10
D. 2 2
Cho các số phức z thỏa mãn i z + 2 - i = 0 Tính khoảng cách từ điểm biểu diễn hình học của z trên mặt phẳng tọa độ Oxy đến điểm M(3; -4)
A. 2 5
B. 13
C. 2 10
D. 2 2
Cho số phức z thỏa mãn: |z|= 4. Tập hợp các điểm trên mặt phẳng tọa độ biểu diễn số phức w thỏa mãn: w = (3+4i)z + i là một đường tròn có bán kính là:
A. 4.
B. 5.
C. 20.
D. 22.
Tập hợp các điểm M trên mặt phẳng tọa độ biểu diễn các số phức z thỏa mãn điều kiện z + z ¯ + 3 = 4 là
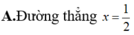
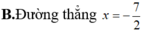
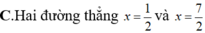
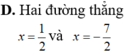
Trên mặt phẳng tọa độ Oxy, tập hợp các điểm biểu diễn các số phức z thỏa mãn điều kiện z i - 1 - 2 i = 4 là
![]()
![]()
![]()
![]()
Trên mặt phẳng tọa độ Oxy, tập hợp các điểm biểu diễn các số phức z thỏa mãn điều kiện z i - 1 - 2 i = 4 là
![]()
![]()
![]()
![]()
Trên mặt phẳng tọa độ Oxy, tìm tập hợp các điểm M biểu diễn số phức z thỏa mãn z - ( 3 - 4 i ) = 2
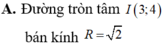
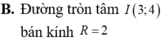
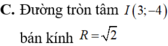
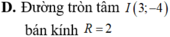
Số phức z = a + bi được biểu diễn trên mặt phẳng phức là tiếp điểm của một tiếp tuyến đi qua gốc tọa độ O(0;0) với đường tròn
(C): x - 3 2 + y - 4 2 = 4 trên mặt phẳng phức đó. Khoảng cách từ O đến tiếp điểm bằng
![]()
![]()
![]()
![]()