Giải phương trình sau:
4x+12.2x=32
Những câu hỏi liên quan
Khi đặt
t
2
x
, phương trình
4
x
+
1
−
12.2
x
−
2
−
7
0
trở thành phương trình nào sau đây? A.
t
2
−
3
t
−
7...
Đọc tiếp
Khi đặt t = 2 x , phương trình 4 x + 1 − 12.2 x − 2 − 7 = 0 trở thành phương trình nào sau đây?
A. t 2 − 3 t − 7 = 0
B. 4 t 2 − 12 t − 7 = 0
C. 4 t 2 − 3 t − 7 = 0
D. t 2 − 12 t − 7 = 0
Đáp án C
Ta có: 4 x + 1 − 12.2 x − 2 − 7 = 0
⇔ 4.4 x − 12. 2 x 4 − 7 = 0 → t = 2 x 4. t 2 − 3 t − 7 = 0
Đúng 0
Bình luận (0)
4x-12.2x+32=0
x2 - 4x + 4 = 25 <=> (x -2)2 = 52
x - 2 = 5 hoặc x - 2 = - 5 => x = 7 hoặc x = - 3
Đúng 0
Bình luận (0)
(x-2)^2-5^2=0
(x-2-5)(x-2+5)=0
(x-7)(x+3)=0
x=7;x=-3
Đúng 0
Bình luận (0)
4xn+12.2xn=32
\(4x^n+12.2x^n=32\)
\(4x^n+24x^n=32\)
\(28x^n=32\)
\(x^n=\frac{8}{7}\)
\(x=\sqrt[n]{\frac{8}{7}}\)
Đúng 0
Bình luận (0)
Giải hệ bất phương trình sau:
6
x
+
5
7
4
x
+
7...
Đọc tiếp
Giải hệ bất phương trình sau: 6 x + 5 7 < 4 x + 7 8 x + 3 2 < 2 x + 5
ập xác định D = R.
Giải từng bất phương trình ta có:
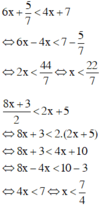
Vậy tập nghiệm của hệ bất phương trình là
Đúng 0
Bình luận (0)
Giải các phương trình sau:
a
)
12
x
2
+
30
x
-
21
16
x
2
-
9
-
3
x
-
7
3
-
4
x...
Đọc tiếp
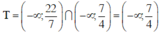
Giải các phương trình sau:
a ) 12 x 2 + 30 x - 21 16 x 2 - 9 - 3 x - 7 3 - 4 x = 6 x + 5 4 x + 3
b ) x + 3 2 - x - 3 2 = 6 x + 18
a) ĐKXĐ : 3 – 4x ≠ 0 và 3 + 4x ≠ 0 (16x2 – 9 = - (3 – 4x)(3 + 4x) ≠ 0)
⇔ x ≠ 3/4 và x ≠ -3/4
Quy đồng mẫu thức :
Khử mẫu, ta được :
-12x2 – 30x + 21 – (9x + 12x2 – 21 – 28x) = 18x – 24x2 + 15 – 20x
⇔ -12x2 – 30x + 21 – 9x – 12x2 + 21 + 28x = 18x – 24x2 + 15 – 20x
⇔ -9x = -27 ⇔ x = 3 (thỏa mãn ĐKXĐ)
Tập nghiệm : S = {3}
b) (x + 3)2 - (x -3)2 = 6x + 18
⇔ x2 + 6x + 9 – x2 + 6x – 9 = 6x + 18
⇔ 6x = 18 ⇔ x = 3
Tập nghiệm : S = {3}
Đúng 0
Bình luận (0)
Tổng các nghiệm của phương trình
x
−
1
2
.2
x
2
x
x
2
−
1
+
4
2
x
−
1
−...
Đọc tiếp
Tổng các nghiệm của phương trình x − 1 2 .2 x = 2 x x 2 − 1 + 4 2 x − 1 − x 2 bằng
A. 4
B. 5
C. 2
D. 3
Đáp án A
Phương trình đã cho tương đương
x − 1 2 .2 x = 2 x 3 − 2 x + 2.2 x − 4 x 2 ⇔ x 2 − 2 x − 1 2 x = 2 x x 2 − 2 x − 1 ⇔ x 2 − 2 x − 1 = 0 2 x = 2 x ⇔ x 1 + x 2 = 2 2 x − 2 x = 0 *
Đặt f x = 2 x − 2 x ; x ∈ 0 ; + ∞
Ta có:
f ' x = 2 x ln 2 − 2 ⇒ f ' ' x = 2 x ln 2 2 > 0 ; ∀ x ∈ 0 ; + ∞ → f ' x = 0
có nhiều nhất 1 nghiệm ⇒ f ' x = 0 có nhiều nhất 2 nghiệm
Mà f 1 = f 2 = 0 ⇒ x = 0 x = 2 là nghiệm của phương trình
Vậy tổng các nghiệm của phương trình đã cho bằng 4
Đúng 1
Bình luận (0)
Giải các phương trình sau:
a
)
5
x
-
3
2
4
x
-
7
2
*
b
)
96
x
2
-
16
+
6
2...
Đọc tiếp
Giải các phương trình sau:
a ) 5 x - 3 2 = 4 x - 7 2 * b ) 96 x 2 - 16 + 6 = 2 x - 1 x + 4 + 3 x - 1 x - 4 c ) 1 - x 2 x 2 - 4 x - 1 4 x - 4 = x - 1 2 x x - 2 - 1 2 x
a) (*) ⇔ (5x – 3)2 – (4x – 7)2 = 0
⇔ (5x – 3 + 4x – 7)(5x – 3 – 4x + 7) = 0
⇔ (9x – 10)(x + 4) = 0 ⇔ 9x – 10 = 0 hoặc x + 4 = 0
⇔ x = 10/9 hoặc x = -4
Tập nghiệm : S = { 10/9 ; -4}
b) ĐKXĐ: (x + 4)(x – 4) ≠ 0 ⇔ x + 4 ≠ 0 và x – 4 ≠ 0 ⇔ x ≠ ⇔ 4
Ta có: x2 – 16 = (x + 4)(x – 4) ≠ 0
Quy đồng và khử mẫu, ta được:
96 + 6(x2 – 16) = (2x – 1)(x – 4) + (3x – 1)(x + 4)
⇔ 96 + 6x2 – 96 = 2x2 – 8x – x + 4 + 3x2 + 12x – x – 4
⇔ x2 – 2x = 0 ⇔ x(x – 2) = 0
⇔ x = 0 hoặc x – 2 = 0
⇔ x = 0 hoặc x = 2 (thỏa mãn ĐKXĐ)
Tập nghiệm: S = {0;2}
c) ĐKXĐ: x ≠ 0; x – 1 ≠ 0 và x – 2 ≠ 0 ⇔ x ≠ 0; x ≠ 1 và x ≠ 2
MTC: 4x(x – 2)(x – 1)
Quy đồng và khử mẫu, ta được:
2(1 – x)(x – 1) – x(x – 2) = 2(x – 1)2 – 2(x – 1)(x – 2)
⇔ -2x2 + 4x – 2 – x2 + 2x = 2x2 – 4x + 2 – 2x2 + 6x – 4
⇔ 3x2 – 4x = 0 ⇔ x(3x – 4) = 0 ⇔ x = 0 hoặc x = 4/3
(x = 0 không thỏa mãn ĐKXĐ)
Tập nghiệm: S = {4/3}
Đúng 0
Bình luận (0)
Bài 1: Giải các bất phương trình và phương trình sau :
a) 2(3-4x) = 10-(2x – 5)
Giải các bất phương trình và phương trình sau :
a) 3(2-4x) = 11-(3x – 1)
Bài 1:
a) Ta có: \(2\left(3-4x\right)=10-\left(2x-5\right)\)
\(\Leftrightarrow6-8x-10+2x-5=0\)
\(\Leftrightarrow-6x+11=0\)
\(\Leftrightarrow-6x=-11\)
hay \(x=\dfrac{11}{6}\)
b) Ta có: \(3\left(2-4x\right)=11-\left(3x-1\right)\)
\(\Leftrightarrow6-12x-11+3x-1=0\)
\(\Leftrightarrow-9x-6=0\)
\(\Leftrightarrow-9x=6\)
hay \(x=-\dfrac{2}{3}\)
Đúng 2
Bình luận (0)
Chứng minh bất phương trình sau vô nghiệm:
1
+
2
x
-
3
2
+
5
-
4
x
+
...
Đọc tiếp
Chứng minh bất phương trình sau vô nghiệm: 1 + 2 x - 3 2 + 5 - 4 x + x 2 < 3 2
Tập xác định: D = R.
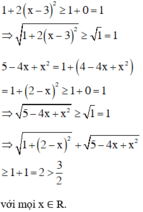
Do đó BPT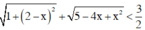 
vô nghiệm.
Đúng 0
Bình luận (0)
Giải các phương trình sau:a)
x
−
2
2
−
2
x
+
3
2
0
;b)
9
2
x
+
1
2
−
4...
Đọc tiếp
Giải các phương trình sau:
a) x − 2 2 − 2 x + 3 2 = 0 ;
b) 9 2 x + 1 2 − 4 x + 1 2 = 0 ;
c) x + 1 2 + 2 x + 1 + 1 = 0 ;
d) x − 1 x 2 − 9 + x + 3 = 0 .
