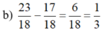\(\Rightarrow4A=4+4^2+4^3+...+4^{100}\\ \Rightarrow4A-A=\left(4+4^2+4^3+...+4^{100}\right)-\left(1+4+4^2+...+4^{99}\right)\\ \Rightarrow3A=4^{100}-1< 4^{100}=B\\ \Rightarrow A< \dfrac{B}{3}\)

\(S=\left(1+4\right)+\left(4^2+4^3\right)+...+\left(4^{98}+4^{99}\right)\\ S=\left(1+4\right)+4^2\left(1+4\right)+...+4^{98}\left(1+4\right)\\ S=\left(1+4\right)\left(1+4^2+...+4^{98}\right)=5\left(1+4^2+...+4^{98}\right)⋮5\)

\(S=\left(1+4\right)+...+4^{98}\left(1+4\right)\)

\(=5\left(1+...+4^{98}\right)⋮5\)

a, (a+b) -( b+c) +(a+c)

= a +b-b-c +a+c

= 2a

tính

a, bỏ ngoặc ta đc giá trị là 70

b giá trị là 50-2

=48

chúc bn học giỏi

a) (a +b) - (b+c) +(a+c)

= a+b-b-c+a+c

= (a+a)+(b-b)+(c-c)

= 2a+0+0

=2a

b) a+(42+70+18)-(42+18+a)

= a+42+70+18-42-18-a

=(a-a)+(42-42)+(18-18)+70

=0+0+0+70

=70

C) a+30+12-(-20)+(-12)-(2+a)

=a+30+12+20-12-2-a

=(a-a)+(12-12)+(30+20-2)

=0+0+48

=48

Bài 2: 

b) Gọi \(d\inƯC\left(21n+4;14n+3\right)\)

\(\Leftrightarrow\left\{{}\begin{matrix}21n+4⋮d\\14n+3⋮d\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}42n+8⋮d\\42n+9⋮d\end{matrix}\right.\)

\(\Leftrightarrow1⋮d\)

\(\Leftrightarrow d\inƯ\left(1\right)\)

\(\Leftrightarrow d\in\left\{1;-1\right\}\)

\(\LeftrightarrowƯCLN\left(21n+4;14n+3\right)=1\)

hay \(\dfrac{21n+4}{14n+3}\) là phân số tối giản(đpcm)

Bài 1: 

a) Ta có: \(A=1+2-3-4+5+6-7-8+...-299-300+301+302\)

\(=\left(1+2-3-4\right)+\left(5+6-7-8\right)+...+\left(297+298-299-300\right)+301+302\)

\(=\left(-4\right)+\left(-4\right)+...+\left(-4\right)+603\)

\(=75\cdot\left(-4\right)+603\)

\(=603-300=303\)

Bài 1: 

c) Ta có: \(B=\dfrac{1}{3}+\dfrac{1}{3^2}+...+\dfrac{1}{3^{99}}\)

\(\Leftrightarrow3B=1+\dfrac{1}{3}+...+\dfrac{1}{3^{98}}\)

\(\Leftrightarrow3B-B=1+\dfrac{1}{3}+...+\dfrac{1}{3^{98}}-\dfrac{1}{3}-\dfrac{1}{3^2}-...-\dfrac{1}{3^{98}}-\dfrac{1}{3^{99}}\)

\(\Leftrightarrow2B=1-\dfrac{1}{3^{99}}\)

\(\Leftrightarrow B=\dfrac{3^{99}-1}{3^{99}\cdot2}\)

Bài 2: 

a) Vì tổng của hai số là 601 nên trong đó sẽ có 1 số chẵn, 1 số lẻ

mà số nguyên tố chẵn duy nhất là 2

nên số lẻ còn lại là 599(thỏa ĐK)

Vậy: Hai số nguyên tố cần tìm là 2 và 599

b,Gọi ƯCLN(21n+4,14n+3)=d

21n+4⋮d ⇒42n+8⋮d

14n+3⋮d ⇒42n+9⋮d

(42n+9)-(42n+8)⋮d

1⋮d ⇒ƯCLN(21n+4,14n+3)=1

Vậy phân số 21n+4/14n+3 là phân số tối giản

c,xy-2x+5y-12=0

xy-2x+5y-12+2=0+2

xy-2x+5y-10=2

xy-2x+5y-5.2=-2

x.(y-2)+5.(y-2)=2

(y-2).(x+5)=2

Sau đó bạn tự lập bảng 

`41xx11-4100xx0,1-4100xx0,01`

`=41xx11-41xx10-41xx1`

`=41xx(11-10-1)=41xx0=0`

410 + 41 - 410 - 41 = 0

há

Kết quả 0

a) 407 + 24 + (-407) + (-84)

= [407 + (-407)] + 24 + (-84)

= 0 + 24 + (-84)

= 24 + (-84)

= (-60)

b) (-42) x 23 + 77 x (-42) - 200

= (-42) x (23 + 77) - 200

= (-42) x 100 - 200

= (-4200) - 200

= (-4400)

c) (-2021) + (499 + 2021) + 41

= (-2021) + 499 + 2021 + 41

= [(-2021) + 2021] + 499 + 41

= 0 + 499 + 41

= 499 + 41

= 540

d) (-202) - (34 - 202) - 66 + 50

= (-202) - 34 + 202 - 66 + 50

= [(-202) + 202] - 34 - 66 + 50

= 0 - 34 - 66 + 50

= (-34) - 66 + 50

= (-100) + 50

= (-50)

e) Bạn viết lại đề bài.

Gọi phân số cần tìm là a/b.

Theo bài ra ta có:

a/b = 5/6

a/(b+8) = 3/4

Quy đồng mâu số 2 vế khi đó tử số 2 phân số bằng nhau ta lại có:

6a = 5b (1)

4a = 3b + 24 (2)

Dùng phương pháp thế khử: Nhân 2 vế của (1) với 3; nhân 2 vế của (2) với 5 ta có:

18a = 15b (3)

20a = 15b + 120 (4)

Trừ (4) cho (3) vế theo vế ta có: 2a = 120 => a = 60

Thay a = 60 vào (1) ta tính được b = 72

Vậy phân số cần tìm là 60/72

Cách khác: a/b = 5/6; a/b+8 = 3/4.

Ta có: a/b : a/b+8 = 5/6:3/4

   Hay: b+8/b = 10/9

Dùng cách qui đồng mẫu số cho tử số bằng nhau ta được:

(b+8)x9 = bx10

Giải ra ta được b = 72 từ đó tìm được a = 60. PS là 60/72
Chúc bạn học tốt! (^ _ ^)

Gọi phân số cần tìm là a/b.

Theo bài ra ta có:

a/b = 5/6

a/(b+8) = 3/4

Quy đồng mâu số 2 vế khi đó tử số 2 phân số bằng nhau ta lại có:

6a = 5b (1)

4a = 3b + 24 (2)

Dùng phương pháp thế khử: Nhân 2 vế của (1) với 3; nhân 2 vế của (2) với 5 ta có:

18a = 15b (3)

20a = 15b + 120 (4)

Trừ (4) cho (3) vế theo vế ta có: 2a = 120 => a = 60

Thay a = 60 vào (1) ta tính được b = 72

Vậy phân số cần tìm là 60/72

Cách khác: a/b = 5/6; a/b+8 = 3/4.

Ta có: a/b : a/b+8 = 5/6:3/4

   Hay: b+8/b = 10/9

Dùng cách qui đồng mẫu số cho tử số bằng nhau ta được:

(b+8)x9 = bx10

Giải ra ta được b = 72 từ đó tìm được a = 60. PS là 60/72

hi hi kem đánh răng P/S

A HI HI