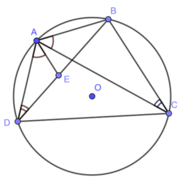
Cho tứ giác ABCD nội tiếp đường tròn (O) . Chứng minh rằng : AC.BD ≤ AB.CD + AD.BC .

Những câu hỏi liên quan
cho tứ giác ABCD nội tiếp đường tròn (O). Chứng minh AB.CD+AD.BC=AC.BD
Ta có: `hat(ABD) = hat(ACD)`.
Lấy `M in AC` sao cho `hat(ADB) = hat(MDC)`.
`=> triangle ABD ~ triangle MCD`.
`=> (AB)/(MC) = (BD)/(CD) => AB . CD = BD . MC`.
Xét `2 triangle ADM, BDC`, ta có:
`hat(ADM) = hat(BDC)`.
`(DA)/(DM) = (BD)/(DC) ( triangle ABD ~ triangle MCD )`.
`=> triangle ADM ~ triangle BCD => (AD)/(AM) = (BD)/(CB) => AD . BC = BD . AM`
`=> AD . BC + AD . BC = BD . AM + BD . MC`
`=> AD . BC + AD . BC = BD(AM+MC)`
`=> AD.BC+AD.BC = BD . AC => dpcm`.
Đúng 3
Bình luận (3)
Cho tứ giác ABCD nội tiếp đường tròn tâm ( O ) Chứng minh AB.CD+AD.BC=AC.BD
Cho tứ giác ABCD nội tiếp đường tròn (O). Trên đường chéo BD lấy điểm E sao cho ∠ DAE = ∠ BAC . Chứng minh: AD.BC + AB.CD = AC.BD
Cho tứ giác ABCD nội tiếp dường tròn (O). Chứng minh: AC.BD = AB.CD + AD.BC
vì tứ giác ABCD nội tiếp,theo định lý Ptoleme ta có:
AC.BD=AB.CD+AD.BC (ĐPCM)
Đúng 0
Bình luận (0)
Cho tứ giác ABCD nội tiếp đường tròn (O).
Chứng minh : AC.BD = AB.CD + AD.BC
Giả sử BCD là tam giác đều có cạnh bằng Chứng tỏ AC = AB + AD và tính diện tích hình quạt tròn OBC .
Cho tứ giác ABD nội tiếp trong vòng tròn (o). CM : AC.BD = AB.CD + AD.BC
Cho tứ giác ABCD nội tiếp đường tròn tâm (0). Chứng minh AB.CD+ AD.BC=AC.BD
Help me
cho t/g nội tiếp ABCD
khi đó <BAC= <BDC VÀ <ADB = <ACB
DỰNG K TRÊN AC SAO CHO <ABK = <CBD
VÌ <ABK+ <CBK=<ABC= <CBD+ <ABD NÊN <CBK= <ABD
➙△ABK∼△DBC VÀ △ABD∼△KBC
➙AK/AB=CD/BD VÀ CK/BC=DA/BC
➙AK*BD=AB*CD VÀ CK*BD =BC*DA
CỘNG LẠI ĐƯỢC:AK*BD+CK*BD=AB*CD+BC*DA
NHÓM NHÂN TỬ:(AK+CK)*BD=AB*CD+BC*DA
MÀ AK+CK=AC
VẬY AC*BD=AB*CD+BC*DA(đpcm)
Đúng 0
Bình luận (0)
Cho tứ giác ABCD nội tiếp (O)
C/m : AB.CD + AD.BC = AC.BD
Ta có ABCD là tứ giác nội tiếp đường tròn.
Trên cung nhỏ BC, ta có các góc nội tiếp ∠BAC = ∠BDC, và trên cung AB, ∠ADB = ∠ACB.
Lấy 1 điểm K trên AC sao cho ∠ABK = ∠CBD;
Từ ∠ABK + ∠CBK = ∠ABC = ∠CBD + ∠ABD, suy ra ∠CBK = ∠ABD.
Do vậy tam giác △ABK đồng dạng với tam giác △DBC, và tương tự có △ABD ∼ △KBC.
Suy ra: AK/AB = CD/BD, và CK/BC = DA/BD;
Từ đó AK·BD = AB·CD, và CK·BD = BC·DA;
Cộng các vế của 2 đẳng thức trên: AK·BD + CK·BD = AB·CD + BC·DA;
Hay: (AK+CK)·BD = AB·CD + BC·DA;
Mà AK+CK = AC, nên AC·BD = AB·CD + BC·DA; (điều phải chứng minh)
Đúng 0
Bình luận (0)
Cho đường tròn tâm O , đường thẳng d cắt đường tròn tâm O tại A và B . Từ điểm M thuộc d kẻ tiếp tuyến MC và MD của đường tròn a) chứng minh tứ giác MCOD nội tiếp b) chứng minh tam giác MCA đồng dạng tam giác MBC c) chứng minh AC.BD=AD.BC
a: Xét tứ giác MCOD có \(\widehat{MCO}+\widehat{MDO}=180^0\)
nên MCOD là tứ giác nội tiếp
b: Xét ΔMCA và ΔMBC có
\(\widehat{MCA}=\widehat{MBC}\)
\(\widehat{AMC}\) chung
Do đó; ΔMCA\(\sim\)ΔMBC
Đúng 0
Bình luận (0)