Các câu hỏi tương tự
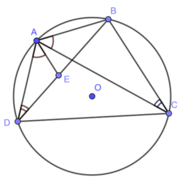
Cho tứ giác ABCD nội tiếp đường tròn (O). Trên đường chéo BD lấy điểm E sao cho ∠ DAE = ∠ BAC . Chứng minh: ∆ ADE ~ ∆ ACE, ∆ ABE ~ ∆ ACD
cho tứ giác ABCD nội tiếp đường tròn (O). Chứng minh AB.CD+AD.BC=AC.BD
Cho tứ giác ABCD nội tiếp đường tròn tâm ( O ) Chứng minh AB.CD+AD.BC=AC.BD
Cho tứ giác ABCD nội tiếp dường tròn (O). Chứng minh: AC.BD = AB.CD + AD.BC
Cho tứ giác ABCD nội tiếp đường tròn (O).
Chứng minh : AC.BD = AB.CD + AD.BC
Giả sử BCD là tam giác đều có cạnh bằng Chứng tỏ AC = AB + AD và tính diện tích hình quạt tròn OBC .
Cho ABCD là tứ giác nội tiếp đường tròn (O). Trên đường chéo BD lấy điểm
E sao cho EAB = CAD
Cmr:
a) ∆ABE ~ ∆ACD;
b) AD.BC = AC.DE
c) AB. CD + AD. BC = AC. BD
Cho đường tròn tâm O , đường thẳng d cắt đường tròn tâm O tại A và B . Từ điểm M thuộc d kẻ tiếp tuyến MC và MD của đường tròn a) chứng minh tứ giác MCOD nội tiếp b) chứng minh tam giác MCA đồng dạng tam giác MBC c) chứng minh AC.BD=AD.BC
Cho tứ giác ABD nội tiếp trong vòng tròn (o). CM : AC.BD = AB.CD + AD.BC
Cho tứ giác ABCD nội tiếp đường tròn đường kính AB. Hai đường chéo AC và BD vắt nhau tại E , F là hình chiếu vuông góc của E trên ABa Chứng minh tứ giác ADEF nội tiếpb Gọi N là giao điểm của CF và BD. Chứng minh BN.ED BD.EN