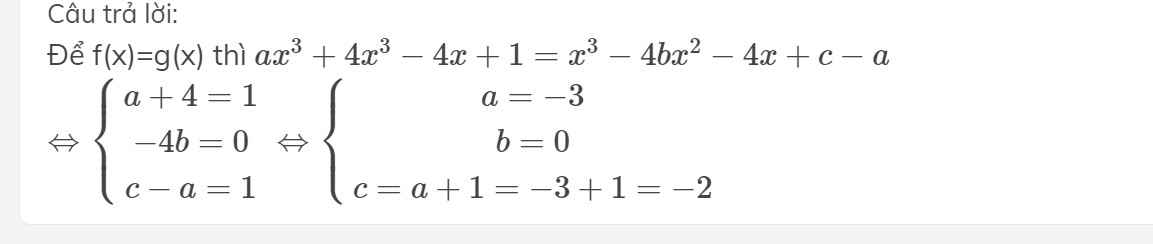tim a,b biet f(x) chia het cho g(x):f(x)=x^4+a.x+b;g(x)=x^2-9

Những câu hỏi liên quan
cho f(x)=a.x^2+b.x+c .Biet f(1)=2 ; f(3)=8 .Tim a;b?
cho f(x) = 2x^2+ax+4
g(x) = x^2-5x-b
tim a , b biet f(1)=g(2) ; f(-1)=g(5)
Ta có: f(1) = 2.12 + a . 1 + 4 = 2 + a + 4 = 6 + a
g(2) = 22 - 5.2 - b = 4 - 10 - b = -6 - b
Mà g(1) = g(2)
hay 6 + a = -6 - b
=> 6 + 6 = -b - a
=> -a - b = 12 (1)
Ta lại có: f(-1) = 2.(-1)2 + a.(-1) + 4 = 2 - a + 4 = 6 - a
g(5) = 52 - 5.5 - b = 25 - 25 - b = -b
Mà f(-1) = g(5)
=> 6 - a = -b
=> 6 = -b + a
=> a - b = 6 (2)
Từ (1) và (2) cộng vế cho vế :
(-a - b) + (a - b) = 6
=> -a - b + a - b = 6
=> -2b = 6
=> b = 6: (-2)
=> b = -3
Thay b = -3 vào (1) ta được :
-a - (-3) = 12
=> -a + 3 = 12
=> -a = 11 => a = -11
Đúng 0
Bình luận (0)
Ta có :
f(1) = 2.12 +a.1 +4 =6a
g(2) = 22 - 5.2 -b = 4-10-b = -b-6
Có : f(1) =g(2) => 6a = -b-6
a = -b-6-6 = -b -12 (1)
f(-1) = 2. (-1)2 +a.(-1)+4 = 2.1 - a +4 = 2-a+4 = 6-a
g(5) = 52 - 5.5 -b= -b
f(1) = g(5) => 6-a = -b
a = 6+b (2)
Từ (1) và (2) => 6+b = b-12
b+b = 12-6
2b = -18
=> b=-9
Thay b=-9 vào (2) => a= 6-9 =-3
Vậy a=-2 , b=9
Đúng 0
Bình luận (0)
Vì f(x) = 2x2 + ax + 4
=> f(1) = 2 . 12 + a . 1 + 4 = 2 + a + 4 = 6 + a
f(-1) = 2 . ( - 1 )2 + a . ( - 1 ) + 4 = 2 - a + 4 = 6 - a
Vì g(x) = x2 - 5x - b
=> g(2) = 22 - 5 . 2 - b = 4 - 10 - b = - 6 - b
g(5) = 52 - 5.5 - b = - b
Mà f(1) = g(2) ; f(-1) = g(5)
=> f(1) + f(-1) = g(2) + g(5)
hay 6 + a + 6 - a = - 6 - b + ( - b )
12 = - 6 - 2b
2b = -18 => b = - 9
Thay vào tính được a = - 3
Vậy ...
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
a, Cho F(x) = a x+b . Tim a,b biet f(0) = 3 va F(2) =-1
b, Cho F(x) =a x+ b. Tim a,b biet F(1) = -1 va F(-2) = 8
c, Cho F(x) =a x +b .tim a,b biet F(0) = 1 va F(-2) = -9
bai 1 : tim x E n bieta ( 9 + 8 )x + 16 . 2x 98b 37.5 mu x - 12. 5 mu x ( 125 mu 2 )mu 3c [27 + 5(x - 4 ) ] chia het cho 9d 90 chia het cho x, 150 chia het cho x va 5x30e x chia het 48, x chia het 36 va x 500f x chia het 60, x chia het 42, va 840x2500g 45 chia het 2x + 1h ( x +16 ) chia het ( x +15 )k ( 2 x + 7 ) chia het ( x - 1 )m ( 3x + 27 ) chia het (2x + 3)n 326 chia cho x du 11 con 553 chia x du 13
Đọc tiếp
bai 1 : tim x E n biet
a ( 9 + 8 )x + 16 . 2x = 98
b 37.5 mu x - 12. 5 mu x = ( 125 mu 2 )mu 3
c [27 + 5(x - 4 ) ] chia het cho 9
d 90 chia het cho x, 150 chia het cho x va 5<x<30
e x chia het 48, x chia het 36 va x< 500
f x chia het 60, x chia het 42, va 840<x<2500
g 45 chia het 2x + 1
h ( x +16 ) chia het ( x +15 )
k ( 2 x + 7 ) chia het ( x - 1 )
m ( 3x + 27 ) chia het (2x + 3)
n 326 chia cho x du 11 con 553 chia x du 13
traa loi nhanh cho minh , minh can gap vao dem thu sau ngay 8 thang 11
Bài 1
a)(9+8)x + 16 . 2x = 98
17x + 32x = 98
49x = 98
x = 98 : 49
x = 2
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
cho f(x)= a.x^3+4.x.(x^2-x)-4x+8 và g(x)= x^3-4.xa.(b.x+1)+c-3 xác đinh a, b để f(x)=g(x)
xac dinh a, b de f(x)=x^4+ax^2+b chia het cho g(x)=x^2+x+1
cho f(x)= a.x^3+4.x.(x^2-x)-4x+8 và g(x)= x^3-4.xa.(b.x+1)+c-3 xác đinh a b để f(x)=g(x)
cho f(x)=a.x^2+b.x+c ; a,b,c thuộc Z biết f(x) chia hết cho 5 với mọi x thuộc Z.CMR a^4+b^1+c^2018 chia hết cho 5
a; Xac dinh a; b de phep chia sau la phep chia het : 5x4+5x3+x2+11x+a chia het cho x2+x+b .Tim thuong voi a; b tim duoc ?
b; Tim x biet : x4-30x2+31x-30=0
Đặt Q là thương của phép chia . Vì đây là phép chia hết nên ta có phương trình
5x4+5x3+x2+11x+a = (x2+x+b)Q . Mà vế trái là đa thức bậc 4 nên khi chia cho đa thức bậc 2 thì thương có dạng Q = mx2+nx+h
( với m,n,h là hệ số của đa thức )
=> 5x4+5x3+x2+11x+a = (x2+x+b)(mx2+nx+h)
<=>5x4+5x3+x2+11x+a = mx4+ nx3 + hx2 + mx3 + nx2 + hx + bmx2 + bnx + bh
= mx4 + (m+n)x3 + (h+n+bm)x2 + (h+bn)x + bh
Mà theo nguyên tắc hai vế bằng nhau thì hệ số của bậc nào bằng hệ số bậc cùng bậc bên vế kia .
=> m = 5
m+n = 5 => n = 0
h+bn = 11 => h = 11
h+n+bm = 1 => b = -2
bh = a = -22
Vậy a = -22 ; b = -2 ; Q = 5x2+11
Đúng 0
Bình luận (0)
x4-30x2+31x-30 = 0
<=> x4 + ( x3 - x3 ) + ( x2 - x2 - 30x2 ) + ( 30x + x ) -30 = 0
<=> ( x4 + x3 - 30x2 ) + ( -x3 - x2 + 30x ) + ( x2 + x - 30 ) =0
<=> x2.( x2 + x - 30 ) - x.( x2 + x - 30 ) + ( x2 + x - 30 ) = 0
<=> ( x2 + x - 30 )( x2 - x + 1 ) = 0
<=> ( x2 + x - 30 )( x - 5 )( x + 6 ) = 0
Vì x2 + x - 30 = x2 + x + \(\frac{1}{4}\) - \(\frac{121}{4}\) = ( x + \(\frac{1}{2}\) )2 - \(\frac{121}{4}\) \(\ge\)- \(\frac{121}{4}\)
=> x - 5 = 0 hoặc x + 6 = 0
=> x = 5 hoặc x = -6
Vậy tập nghiệm S = { -6 ; 5 }
Đúng 0
Bình luận (0)
b) \(x^4-30x^2+31-30=0\)
\(\Leftrightarrow x^4+x-30\left(x^2-x+1\right)=0\)
\(\Leftrightarrow x\left(x^3+1\right)-30\left(x^2-x+1\right)=0\)
\(\Leftrightarrow x\left(x+1\right)\left(x^2-x+1\right)-30\left(x^2-x+1\right)=0\)
\(\Leftrightarrow\left(x^2-x+1\right)\left(x^2+x-30\right)=0\)
\(\Leftrightarrow\left(x+6\right)\left(x-5\right)\left(x^2-x+1\right)=0\)
\(\Leftrightarrow\hept{\begin{cases}x+6=0\\x-5=0\\x^2-x+1=0\end{cases}\Leftrightarrow\hept{\begin{cases}x=-6\\x=5\\\left(x-\frac{1}{2}\right)^2+\frac{3}{4}>0\left(\text{loai}\right)\end{cases}}}\)
\(\Rightarrow x\in\left\{-6;5\right\}\)
Đúng 0
Bình luận (0)