Cho hai số thực a;b thay đổi thỏa mãn điều kiện \(a+b\ge1\) và \(a>0\)
Tìm GTNN của \(A=\frac{8a^2+b}{4a}+b^2\)
Những câu hỏi liên quan
Cho a, b là hai số thực dương và m, n là hai số thực tùy ý. Khẳng định nào sau đây sai? A.
a
m
b
m
a
b
m
B.
a
m
.
a
n
a
m...
Đọc tiếp
Cho a, b là hai số thực dương và m, n là hai số thực tùy ý. Khẳng định nào sau đây sai?
A. a m b m = a b m
B. a m . a n = a m . n
C. a m n = a m . n
D. 1 b − n = b n
Cho a là số thực dương khác 1. Xét hai số thực
x
1
,
x
2
. Phát biểu nào sau đây đúng? A.
N
ế
u
a
x
1
a
x
2
t
h
ì
x
1
x
2...
Đọc tiếp
Cho a là số thực dương khác 1. Xét hai số thực x 1 , x 2 . Phát biểu nào sau đây đúng?
A. N ế u a x 1 > a x 2 t h ì x 1 > x 2 .
B. N ế u a x 1 > a x 2 t h ì x 1 < x 2 .
C. N ế u a x 1 > a x 2 t h ì a − 1 x 1 − x 2 > 0.
D. N ế u a x 1 > a x 2 t h ì a − 1 x 1 − x 2 < 0.
Cho a là số thực dương khác 1. Xét hai số thực
x
1
,
x
2
. Phát biểu nào sau đây đúng? A. Nếu
a
x
1
a
x
2
thì
x
1
x
2
....
Đọc tiếp
Cho a là số thực dương khác 1. Xét hai số thực x 1 , x 2 . Phát biểu nào sau đây đúng?
A. Nếu a x 1 > a x 2 thì x 1 > x 2 .
B. Nếu a x 1 > a x 2 thì x 1 < x 2 .
C. Nếu a x 1 > a x 2 thì a − 1 x 1 − x 2 > 0.
D. Nếu a x 1 > a x 2 thì a − 1 x 1 − x 2 < 0.
Cho số thực a > 0. Căn bậc hai số học của a là:
A. a
B. x = a
C. 2 a
D. 2 a
Đáp án đúng : A
Với số dương a, số a được gọi là căn bậc hai số học của a
Đúng 0
Bình luận (0)
Cho số thực a > 0. Số nào sau dây là căn bậc hai số học của a?
A. a
B. - a
C. 2 a
D. 2 a
Đáp án đúng : A
Với số dương a, số a được gọi là căn bậc hai số học của a
Đúng 0
Bình luận (0)
a) Cho hai số phức z1 = 1 + 2i ; z2 = 2 – 3i . Xác định phần thực và phần ảo của số phức z1 – 2z2 .
b) Cho hai số phức z1 = 2 + 5i ; z2 = 3 – 4i . Xác định phần thực và phần ảo của số phức z1.z2
a) Phần thực z1 – 2z2 là – 3, phần ảo của nó là 8.
b) Phần thực và phần ảo của z1.z2 tương ứng là 26 và 7.
Đúng 0
Bình luận (0)
Cho a, b là hai số thực khác 0. Biết 
. Tính tỉ số
a
b
A. 76/3
B. 4/21
C. 2
D. 76/21
Đáp án B
Phương pháp : Đưa về cùng cơ số.
Cách giải :
Đúng 0
Bình luận (0)
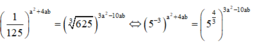
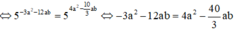
Xác định tính đúng sai của mỗi mệnh đề sau:
a) Nếu \(2a - 1 > 0\) thì \(a > 0\) (a là số thực cho trước).
b) \(a - 2 > b\) nếu và chỉ nếu \(a > b + 2\) (a, b là hai số thực cho trước).
a) Mệnh đề có dạng \(P \Rightarrow Q\) với P: “\(2a - 1 > 0\)” và Q: “\(a > 0\)”
Ta thấy khi P đúng (tức là \(a > \frac{1}{2}\)) thì Q cũng đúng. Do đó, \(P \Rightarrow Q\) đúng.
b) Mệnh đề có dạng \(P \Leftrightarrow Q\) với P: “\(a - 2 > b\)” và Q: “\(a > b + 2\)”
Khi P đúng thì Q cũng đúng, do đó, \(P \Rightarrow Q\) đúng.
Khi Q đúng thì P cũng đúng, do đó, \(Q \Rightarrow P\) đúng.
Vậy mệnh đề \(P \Leftrightarrow Q\) đúng.
Đúng 0
Bình luận (0)
Cho hai số thực dương a, b thỏa mãn
log
a
b
2
. Tính
log
a
b
b
3
.
a
A.
-
10
9
B.
2
3
C.
-
2
9...
Đọc tiếp
Cho hai số thực dương a, b thỏa mãn log a b = 2 . Tính log a b b 3 . a
A. - 10 9
B. 2 3
C. - 2 9
D. 2 15
Đáp án A
Ta có b = a 2 ⇒ P = log a 3 b 6 a 6 b 2 = log a 3 a 12 a 10 = 10 log a - 9 a = - 10 9 .
Đúng 0
Bình luận (0)
Cho biết hai số thực a và b có tổng bằng 3. Khẳng định nào sau đây là đúng về tích của hai số a và b? A. Có giá trị nhỏ nhất là
9
4
B. Có giá trị lớn nhất là
9
4
C. Có giá trị lớn nhất là
3
2
D. Không có giá trị lớn nhất.
Đọc tiếp
Cho biết hai số thực a và b có tổng bằng 3.
Khẳng định nào sau đây là đúng về tích của hai số a và b?
A. Có giá trị nhỏ nhất là 9 4
B. Có giá trị lớn nhất là 9 4
C. Có giá trị lớn nhất là 3 2
D. Không có giá trị lớn nhất.
Vì a + b = 3 nên b = 3 - a . Do đó:
a b = a 3 - a = - a 2 + 3 a = - a 2 - 2 . 3 2 a + 9 4 + 9 4 = - a - 3 2 2 + 9 4 ≤ 9 4 ∀ a
a b = 9 4 ⇔ a = b = 3 2 Vậy giá trị lớn nhất của a.b là 9 4 (đạt được khi a = b = 3 2 ).
Đáp án là B.
Đúng 0
Bình luận (0)