Quan sát Hình 12. Chứng minh rằng:

a) \(\Delta ABH\backsim\Delta DCB\);
b) \(\frac{{BC}}{{BE}} = \frac{{BD}}{{BA}}\).
Quan sát Hình 12.
a) Chứng minh \(\Delta ABC\backsim\Delta A'B'C'\).
b) Tính độ dài cạnh \(B'C'\).
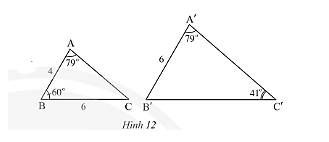
a) Xét tam giác \(A'B'C'\) ta có:
\(\widehat {A'} + \widehat {B'} + \widehat {C'} = 180^\circ \)
Thay số: \(79^\circ + \widehat {B'} + 41^\circ = 180^\circ \)
\( \Rightarrow \widehat {B'} = 180^\circ - 79^\circ - 41^\circ = 60^\circ \)
Xét \(\Delta ABC\) và \(\Delta A'B'C'\) ta có:
\(\widehat A = \widehat {A'} = 79^\circ \) (giả thuyết)
\(\widehat B = \widehat {B'} = 60^\circ \) (chứng minh trên)
Do đó, \(\Delta ABC\backsim\Delta A'B'C'\) (g.g)
b) Vì \(\Delta ABC\backsim\Delta A'B'C'\) nên \(\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}}\) (các cạnh tương ứng có cùng tỉ lệ)
Thay số, \(\frac{4}{6} = \frac{6}{{B'C'}} \Rightarrow B'C' = \frac{{6.6}}{4} = 9\)
Vậy \(B'C' = 9\).
Quan sát Hình 8, cho biết \(DC//MP,EF//MQ\).
a) Chứng minh rằng \(\Delta EPF\backsim\Delta DCQ\).
b) \(\Delta ICF\) có đồng dạng với \(\Delta MPQ\)không? Tại sao?
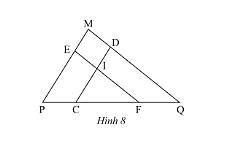
a) Xét tam giác \(MPQ\)có \(EF//MQ\) nên \(\Delta MPQ\backsim\Delta EPF\) (định lí) (1)
Xét tam giác \(MPQ\)có \(DC//MP\) nên \(\Delta MPQ\backsim\Delta DCQ\) (định lí) (2)
Từ (1) và (2) \(\Delta EPF\backsim\Delta DCQ\) (tính chất tam giác đồng dạng)
b) Xét tam giác \(EPF\)có \(IC//EP\) nên \(\Delta ICF\backsim\Delta EPF\) (định lí) (3)
Từ (1) và (3) suy ra, \(\Delta ICF\backsim\Delta MPQ\).
Quan sát Hình 6. Vẽ vào tờ giấy tam giác \(DEF\) với \(EF = 4cm,\widehat E = 36^\circ ,\widehat F = 76^\circ \).
a) Chứng minh \(\Delta DEF\backsim\Delta AMC\).
b) Dùng thước đo chiều dài cạnh \(DF\) của \(\Delta DEF\). Tính khoảng cách giữa hia điểm \(A\) và \(C\) ở hai bờ sông trong Hình 6.

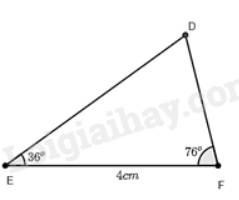
a) Xét tam giác \(DEF\) và tam giác \(AMC\) có:
\(\widehat E = \widehat M = 36^\circ \)
\(\widehat F = \widehat C = 76^\circ \) (chứng minh trên)
Suy ra, \(\Delta DEF\backsim\Delta AMC\) (g.g).
b) Đổi 25m = 2500 cm.
Dùng thước đo độ dài cạnh \(DF\) ta được độ dài \(DF\) là 2,6cm.
Vì \(\Delta DEF\backsim\Delta AMC\) nên \(\frac{{DF}}{{EF}} = \frac{{AC}}{{MC}}\) (hai cặp cạnh tương ứng có cùng tỉ lệ)
Thay số, \(\frac{{2,6}}{4} = \frac{{AC}}{{2500}} \Rightarrow AC = \frac{{2,6.2500}}{4} = 1625\).
Vậy khoảng cách giữa hai điểm \(A\) và \(C\) là 1625 cm hay 16,25m.
Quan sát Hình 4, cho biết \(\Delta ADE\backsim\Delta AMN,\Delta AMN\backsim\Delta ABC,DE\) là đường trung bình của tam giác \(AMN,MN\) là đường trung bình của tam giác \(ABC.\) Tam giác \(ADE\) đồng dạng với tam giác \(ABC\) theo tỉ số đồng dạng là bao nhiêu?
Vì \(\Delta ADE\backsim\Delta AMN\) nên \(\left\{ \begin{array}{l}\widehat A = \widehat A;\widehat {ADE} = \widehat {AMN};\widehat {AED} = \widehat {ANM}\\\frac{{AD}}{{AM}} = \frac{{AE}}{{AN}} = \frac{{DE}}{{MN}}\end{array} \right.\)
Vì \(DE\) là đường trung bình của tam giác \(AMN\)nên \(DE = \frac{1}{2}MN\)
\( \Rightarrow \left\{ \begin{array}{l}\widehat A = \widehat A;\widehat {ADE} = \widehat {AMN};\widehat {AED} = \widehat {ANM}\\\frac{{AD}}{{AM}} = \frac{{AE}}{{AN}} = \frac{{DE}}{{MN}} = \frac{1}{2}\end{array} \right.\)
\( \Rightarrow AM = 2AD;AN = 2AE;MN = 2DE\)
Lại có, \(\Delta AMN\backsim\Delta ABC\) nên \(\left\{ \begin{array}{l}\widehat A = \widehat A;\widehat {AMN} = \widehat {ABC};\widehat {ANM} = \widehat {ACB}\\\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}}\end{array} \right.\)
Vì \(MN\) là đường trung bình của tam giác \(ABC\)nên \(MN = \frac{1}{2}BC\)
\(\left\{ \begin{array}{l}\widehat A = \widehat A;\widehat {AMN} = \widehat {ABC};\widehat {ANM} = \widehat {ACB}\\\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}} = \frac{1}{2}\end{array} \right.\)
\( \Rightarrow AB = 2AM;AC = 2AN;BC = 2MN\)
Vì tam giác \(\Delta ADE\backsim\Delta AMN,\Delta AMN\backsim\Delta ABC,\) nên \(\Delta ADE\backsim\Delta ABC\)
Tỉ số đồng dạng là: \(\frac{{AD}}{{AB}} = \frac{{\frac{{AM}}{2}}}{{2AM}} = \frac{1}{4}\).
Vậy tỉ số đồng dạng là \(\frac{1}{4}\).
Quan sát Hình 3, cho biết \(\Delta AMN\backsim\Delta ABC\).
a) Hãy viết tỉ số của các cạnh tương ứng và tính tỉ số đồng dạng.
b) Tính góc \(\widehat {AMN}\).
a) Vì tam giác \(\Delta AMN\backsim\Delta ABC\) nên ta có \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}}\) (các cạnh tương ứng)
Tỉ số đồng dạng là: \(\frac{{MN}}{{BC}} = \frac{4}{{12}} = \frac{1}{3}\).
b) Vì \(\Delta AMN\backsim\Delta ABC\) nên \(\widehat {AMN} = \widehat {ABC} = 65^\circ \)
Vậy \(\widehat {AMN} = 65^\circ \).
a: AM/AB=AN/AC=MN/BC=4/12=1/3
b: góc AMN=góc ABC=65 độ
Trong Hình 14, cho biết \(AB//CD\)
a) Chứng minh rằng \(\Delta AEB\backsim\Delta DEC\).
b) Tìm \(x\).
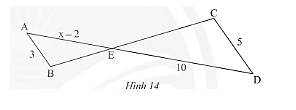
a) Xét tam giác \(ABE\) có:
\(AB//CD\) và \(C,D\) cắt \(BE;AE\) lần lượt tại \(C,D\).
Do đó, \(\Delta AEB\backsim\Delta DEC\) (định lí)
b) Vì \(\Delta AEB\backsim\Delta DEC\) nên \(\frac{{AE}}{{ED}} = \frac{{AB}}{{CD}}\) (các cặp cạnh tương ứng có cùng tỉ lệ).
Thay số ta được:
\(\frac{{x - 2}}{{10}} = \frac{3}{5} \Rightarrow x - 2 = \frac{{10.3}}{5} = 6 \Rightarrow x = 6 + 2 = 8\)
Vậy \(x = 8\).
Cho \(\Delta ABC \backsim \Delta MNP\).
a) Gọi D và Q lần lượt là trung điểm của BC và NP. Chứng minh \(\Delta ABD \backsim \Delta MNQ\).
b) Gọi G và K lần lượt là trọng tâm của hai tam giác ABC và MNP. Chứng minh \(\Delta ABG \backsim \Delta MNK\).
a) Ta có: \(\Delta ABC \backsim \Delta MNP\) suy ra \(\frac{{AB}}{{MN}} = \frac{{BC}}{{NP}}\,\,\left( 1 \right)\) và \(\widehat B = \widehat N\)
Mà D là trung điểm BC và Q là trung điểm NP nên \(BC = 2BD\) và \(NP = 2NQ\)
Thay vào biểu thức (1) ta được \(\frac{{AB}}{{MN}} = \frac{{2BD}}{{2NQ}} \Rightarrow \frac{{AB}}{{MN}} = \frac{{BD}}{{NQ}}\)
Xét tam giác ABD và tam giác MNQ có:
\(\frac{{AB}}{{MN}} = \frac{{BD}}{{NQ}}\) và \(\widehat B = \widehat N\)
\( \Rightarrow \Delta ABD \backsim \Delta MNQ\) (c-g-c)
b) Vì \(\Delta ABD \backsim \Delta MNQ\) nên ta có \(\frac{{AB}}{{MN}} = \frac{{AD}}{{MQ}}\,\,\left( 2 \right)\) và \(\widehat {BAD} = \widehat {NMQ}\) hay \(\widehat {BAG} = \widehat {NMK}\)
Mà G và K lần lượt là trọng tâm của tam giác ABC và tam giác MNP nên \(AD = \frac{3}{2}AG\) và \(MQ = \frac{3}{2}MK\).
Thay vào (2) ta được: \(\frac{{AB}}{{MN}} = \frac{{\frac{3}{2}AG}}{{\frac{3}{2}MK}} \Rightarrow \frac{{AB}}{{MN}} = \frac{{AG}}{{MK}}\)
Xét tam giác ABG và tam giác NMK có:
\(\frac{{AB}}{{MN}} = \frac{{AG}}{{MK}}\) và \(\widehat {BAG} = \widehat {NMK}\)
\( \Rightarrow \)\(\Delta ABG \backsim \Delta MNK\) (c-g-c)
Cho tam giác ABC vuông tại A, đường cao AH (Hình 88). Chứng minh:
a) \(\Delta ABC \backsim \Delta HBA\) và \(A{B^2} = BC.BH\)
b) \(\Delta ABC \backsim \Delta HAC\) và \(A{C^2} = BC.CH\)
c) \(\Delta ABH \backsim \Delta CAH\) và \(A{H^2} = BH.CH\)
d) \(\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}}\)
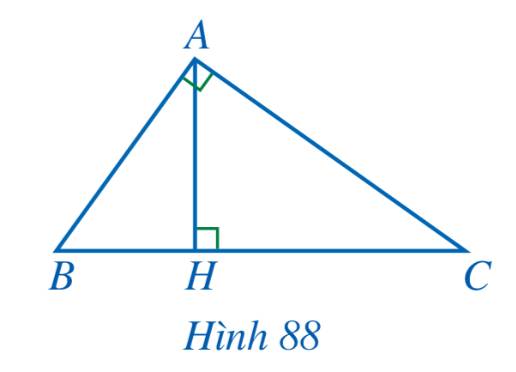
a) Xét tam giác ABC và tam giác HBA có:
\(\widehat {BAC} = \widehat {BHA} = 90^\circ ;\,\,\widehat B\) chung
\( \Rightarrow \Delta ABC \backsim \Delta HBA\) (g-g)
\( \Rightarrow \frac{{AB}}{{HB}} = \frac{{BC}}{{BA}} \Rightarrow A{B^2} = BC.HB\)
b) Xét tam giác ABC và tam giác HAC có:
\(\widehat {BAC} = \widehat {AHC} = 90^\circ ;\,\,\widehat C\) chung
\( \Rightarrow \Delta ABC \backsim \Delta HAC\) (g-g)
\( \Rightarrow \frac{{AC}}{{HC}} = \frac{{BC}}{{AC}} \Rightarrow A{C^2} = BC.CH\)
c) Ta có: \(\Delta ABC \backsim \Delta HBA\) và nên \(\Delta ABH \backsim \Delta CAH\)
\( \Rightarrow \frac{{AH}}{{CH}} = \frac{{BH}}{{AH}} \Rightarrow A{H^2} = BH.CH\)
d) Ta có:
\(A{B^2} = BC.BH \Rightarrow \frac{1}{{A{B^2}}} = \frac{1}{{BC.BH}}\)
\(A{C^2} = BC.CH \Rightarrow \frac{1}{{A{B^2}}} = \frac{1}{{BC.CH}}\)
\(A{H^2} = BH.CH \Rightarrow \frac{1}{{A{H^2}}} = \frac{1}{{BH.CH}}\)
\(\begin{array}{l} \Rightarrow \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}} = \frac{1}{{BC.BH}} + \frac{1}{{BC.CH}}\\ = \frac{1}{{BC}}.\left( {\frac{1}{{BH}} + \frac{1}{{CH}}} \right)\\ = \frac{1}{{BC}}.\frac{{BH + CH}}{{BH.CH}}\\ = \frac{1}{{BC}}.\frac{{BC}}{{BH.CH}}\\ = \frac{1}{{BH.CH}}\\ = \frac{1}{{A{H^2}}}\end{array}\)
Trong Hình 19, cho biết \(MN//BC,MB//AC\)
a) Chứng minh rằng \(\Delta BNM\backsim\Delta ABC\)
b) Tính \(\widehat C\)
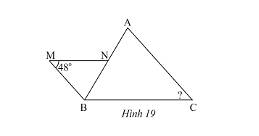
a) Vì \(MN//BC\) nên \(\widehat {MNB} = \widehat {ABC}\) (hai góc so le trong)
Vì \(MB//AC\) nên \(\widehat {MNB} = \widehat {ABC}\) (hai góc so le trong)
Xét tam giác \(BNM\) tam giác \(ABC\) ta có:
\(\widehat {MNB} = \widehat {ABC}\) (chứng minh trên)
\(\widehat {MNB} = \widehat {ABC}\) (chứng minh trên)
Do đó, \(\Delta BNM\backsim\Delta ABC\) (g.g)
b) Vì \(\Delta BNM\backsim\Delta ABC\) nên \(\widehat M = \widehat C = 48^\circ \) (hai góc tương ứng).