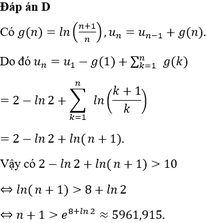cho dãy số U0 =2, U1 =10 ;Un+1 =10Un - Un-1 . Tính U9

Những câu hỏi liên quan
Cho dãy số
u
n
:
u
0
u
1
1
u
n
+
1...
Đọc tiếp
Cho dãy số u n : u 0 = u 1 = 1 u n + 1 = 4 u n - 4 u n - 1 v ớ i m ọ i n ≥ 1
công thức của số hạng tổng quát của dãy số là
A. u n = 1
B. u n = 2 n - n . 2 n - 1
C. u n = - n 2 + n + 1
D. u n = n 2 + 2 n + 3 3 n + 1
Chọn B
Ta có 2n+1 – (n+1)2n= 4(2n – n.2n-1 )- 4(2n-1 – (n-1)2n-2) → un= 2n – n.2n-1
Đúng 0
Bình luận (0)
Cho dãy số
u
n
:
u
0
1
,
u
1
3
u
n...
Đọc tiếp
Cho dãy số u n : u 0 = 1 , u 1 = 3 u n + 1 = 4 u n - 3 u n - 1 v ớ i m ọ i n ≥ 1
Công thức của số hạng tổng quát của dãy số là:
A. u n = 2 n 2 + 1
B. u n = 3 n
C. u n = 2 n + 1
D. u n = ( n + 5 ) / ( n + 1 )
Chọn B
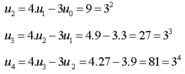
Dự đoán ta được u n = 3 n
Lại có 3 n + 1 = 4.3 n − 3.3 n − 1
Vậy u n = 3 n
Đúng 0
Bình luận (0)
Cho dãy số :
U0 = 1 ; U1 = 2
Un + 2 = 2Un + Un + 1
a ) Tính : U2 + U 3 + U4 + U5
b ) Tính : U10
Cho dãy số (Un) thỏa mãn điều kiện: \(U_{n+1}-2U_n+U_{n-1}=1\) với \(n\ge1\). Hãy tính Un qua U0, U1 và n
Cho dãy số
(
u
n
)
thoả mãn
u
n
u
n
-
1
+
l
n
(
n
+
1
n
)
,
∀
n
≥
2
và
u
1
2...
Đọc tiếp
Cho dãy số ( u n ) thoả mãn u n = u n - 1 + l n ( n + 1 n ) , ∀ n ≥ 2 và u 1 = 2 . Tìm số tự nhiên n nhỏ nhất để u n > 10 .
A. 5962.
B. 5960.
C. 5963.
D. 5961.
Cho dãy số Un được táo thành theo quy tắc sau: mối số sau bằng tích của hai số trước cộng với 1, bắt đầu tử U0=U1=1
a/ lập một quy trình tính Un
b/Có hay không số hạng của dáy chia hết cho 4? Nếu có cho ví dụ? Nếu không háy chững minh?
( toán casio , thanks nhiều)
Cho cấp số nhân (un) biết u1 = 3/2 và q = 1/2. Số u1=3/512 là số hạng thứ mấy của dãy
\(u_n=u_1\cdot q^{n-1}\\ \Rightarrow\dfrac{3}{512}=\dfrac{3}{2}\cdot\left(\dfrac{1}{2}\right)^{n-1}\\ \Leftrightarrow\left(\dfrac{1}{2}\right)^{n-1}=\dfrac{1}{256}\\ \Leftrightarrow\left(\dfrac{1}{2}\right)^{n-1}=\dfrac{1}{2^8}\\ \Leftrightarrow n-1=8\\ \Leftrightarrow n=9\)
Vậy \(\dfrac{3}{512}\) là số hạng thứ 9 của dãy.
Đúng 1
Bình luận (0)
Cho dãy số
(
u
n
)
thỏa mãn
u
1
1
u
n
2...
Đọc tiếp
Cho dãy số ( u n ) thỏa mãn u 1 = 1 u n = 2 u n - 1 + 1 , n ≥ 2 . Tổng S = u 1 + u 2 + . . . + u 20 bằng
A. 2 20 - 20
B. 2 21 - 20
C. 2 20
D. 2 21 - 20
Cho dãy số
(
u
n
)
có
u
1
-
5
,
u
n
+
1
u
n...
Đọc tiếp
Cho dãy số ( u n ) có u 1 = - 5 , u n + 1 = u n + 2 , n ∈ N * . Tổng S 5 = = u 1 + u 2 + . . . + u 5 bằng
A. 5
B. – 5
C. – 15
D. – 24
Chọn B.
Phương pháp:
Công thức tính tổng n số hạng đầu tiên của cấp số cộng có số hạng đầu u1 và công sai d
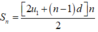
Cách giải:
Ta có: u n + 1 = u n + 2 , ∀ n ∈ ℕ *
⇒ ( u n ) là cấp số cộng có u 1 = - 5 , d = 2
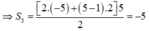
Đúng 0
Bình luận (0)
Cho dãy số
u
n
thỏa mãn
u
1
1
u
n
-
2
u
n
-...
Đọc tiếp
Cho dãy số u n thỏa mãn u 1 = 1 u n - 2 u n - 1 + 1 , n ≥ 2 . Tổng S = u 1 + u 2 + . . . + u 20 bằng
A. 2 20 - 20
B. 2 21 - 22
C. 2 20
D. 2 21 - 20