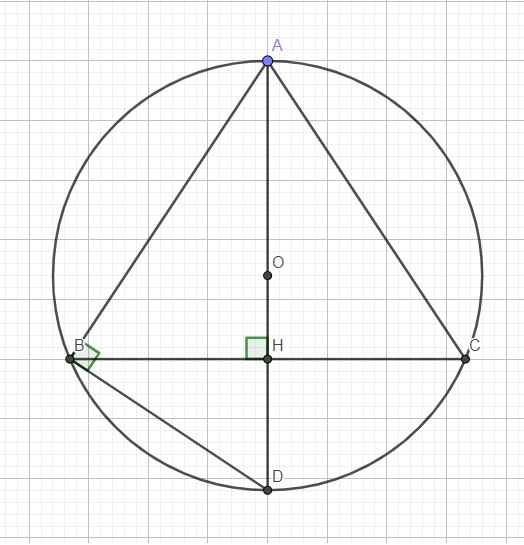
cho tam gáic đều ABC, đường cao AH ngoại tiếp đường tròn (O;R). cho tam giác và đường tròn quay một vòng quanh đường thẳng AH, ta được một hình nón ngoại tiếp một hình cầu. biết AH=2\(\sqrt{2}\) cm. tính diện tích mặt cầu

Những câu hỏi liên quan
Cho tam giác ABC cân tại A nội tiếp đường tròn (O), cạnh AB = a, đường cao AH = h. Tính
bán kính đường tròn ngoại tiếp tam giác theo a và h.
Cho tam giác ABC cân tại A, AB = AC = 6cm, đường cao AH = 5cm.Gọi (O) là đường tròn ngoại tiếp tam giác ABC.
a) Vì sao điểm O nằm trên đường thẳng AH?
b) Tính độ dài đường kính AD của đường tròn (O).
Do tam giác ABC cân tại A nên AH là đường cao đồng thời là trung trực của BC
Mà tâm của đường tròn ngoại tiếp là giao của 3 đường trung trực hay tâm O nằm trên 3 đường trung trực
\(\Rightarrow O\in AH\)
Do AD là đường kính \(\Rightarrow\widehat{ABD}\) là góc nội tiếp chắn nửa đường tròn
\(\Rightarrow\Delta ABD\) vuông tại B
Áp dụng hệ thức lượng:
\(AB^2=AH.AD\Rightarrow AD=\dfrac{AB^2}{AH}=7,2\left(cm\right)\)
Đúng 3
Bình luận (0)
Cho tam giác ABC cân tại A, AB = AC = 6cm, đường cao AH = 5cm. Gọi (O) là đường tròn ngoại tiếp tam giác ABC.
a) Vì sao điểm O nằm trên đường thẳng AH?
b) Tính độ dài đường kính AD của đường tròn (O).
Cho tam giác ABC cân kẻ đường cao AH cắt đường tròn tâm O ngoại tiếp tam giác tại D
a/ c/m AD là đường kính
a) Vẽ tam giác đều ABC cạnh a = 3cm.
b) Vẽ tiếp đường tròn (O; R) ngoại tiếp tam giác đều ABC. Tính R.
c) Vẽ tiếp đường tròn (O; r) nội tiếp tam giác đều ABC. Tính r.
d) Vẽ tiếp tam giác đều IJK ngoại tiếp đường tròn (O; R).
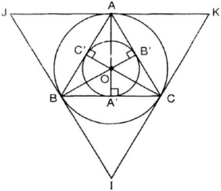
a) Vẽ tam giác đều ABC có cạnh bằng 3cm (dùng thước thẳng và compa).
+ Dựng đoạn thẳng AB = 3cm .
+Dựng cung tròn (A, 3) và cung tròn (B, 3). Hai cung tròn này cắt nhau tại điểm C.
Nối A với C, B với C ta được tam giác đều ABC cạnh 3cm.
b) * Vẽ đường tròn:
Tâm O của đường tròn ngoại tiếp tam giác đều ABC là giao điểm của ba đường trung trực.
Dựng đường trung trực của đoạn thẳng BC và CA.
Hai đường trung trực cắt nhau tại O.
Vẽ đường tròn tâm O, bán kính OA = OB = OC ta được đường tròn ngoại tiếp tam giác ABC.
* Tính bán kính đường tròn.
+ Gọi A’ là trung điểm BC ⇒ A’C = BC/2 = a/2.
và AA’ ⊥ BC
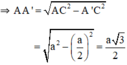
+ Do tam giác ABC là tam giác đều nên 3 đường trung trực đồng thời là ba đường trung tuyến
=> Giao điểm ba đường trung trực cũng là giao điểm ba đường trung tuyến
Suy ra O là trọng tâm tam giác ABC.
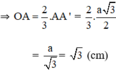
Vậy R = √3 (cm).
c) * Vẽ đường tròn:
Gọi A’; B’; C’ lần lượt là chân đường phân giác trong ứng với các góc 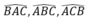
Do tam giác ABC là tam giác đều nên A’; B’; C’ đồng thời là trung điểm BC; CA; AB.
Đường tròn (O; r) là đường tròn tâm O; bán kính OA’ = OB’ = OC’.
* Tính r:
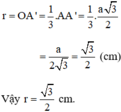
d) Vẽ các tiếp tuyến với đường tròn (O; R) tại A, B, C. Ba tiếp tuyến này cắt nhau tại I, J, K. Ta có ΔIJK là tam giác đều ngoại tiếp (O; R).
Đúng 0
Bình luận (2)
cho tam giác ABC nhọn, CM là đường trung tuyến. 3 đường cao AH,BD,CF cắt nhau tại I, E là trung điểm của DH. kẻ CP song song với AH, cắt BD tại P. kẻ CQ song song với BD, cắt AH tại R. kẻ đường tròn (O) ngoại tiếp tam giác CDHa, CMR:PI.ABIC.ACb, CMR:MD là tiếp tuyến của đường tròn Oc, kẻ CE cắt đường tròn ngoại tiếp tam giác ABC tại R,CM cắt đường tròn (O) tại KCMR: AB là đường trung trực của KR
Đọc tiếp
cho tam giác ABC nhọn, CM là đường trung tuyến. 3 đường cao AH,BD,CF cắt nhau tại I, E là trung điểm của DH. kẻ CP song song với AH, cắt BD tại P. kẻ CQ song song với BD, cắt AH tại R. kẻ đường tròn (O) ngoại tiếp tam giác CDH
a, CMR:PI.AB=IC.AC
b, CMR:MD là tiếp tuyến của đường tròn O
c, kẻ CE cắt đường tròn ngoại tiếp tam giác ABC tại R,CM cắt đường tròn (O) tại K
CMR: AB là đường trung trực của KR
Cho tam giác ABC (AB=AC). kẻ đường cao AH cắt đường tròn tâm O ngoại tiếp tam giác tại D.Chứng minh AD là đường kính.
Cho các đường tròn nội tiếp và ngoại tiếp tam giác đều ABC quay quanh đường cao AH của tam giác tạo nên các khối tròn xoay có thể tích lần lượt là V1, V2. Tính tỉ số
V
1
V
2
Đọc tiếp
Cho các đường tròn nội tiếp và ngoại tiếp tam giác đều ABC quay quanh đường cao AH của tam giác tạo nên các khối tròn xoay có thể tích lần lượt là V1, V2. Tính tỉ số V 1 V 2
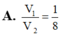
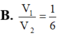
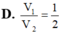
a) Vẽ tam giác đều ABC cạnh a = 3 cm.
b) Vẽ tiếp đường tròn (O; R) ngoại tiếp tam giác đều ABC. Tính R.
c) Vẽ tiếp đường tròn (O; r) nội tiếp tam giác đều ABC. Tính r.
d) Vẽ tiếp tam giác đều IJK ngoại tiếp đường tròn (O ; R).

a) Vẽ tam giác đều ABC có cạnh bằng 3cm (dùng thước có chia khoảng và compa)
b) Tâm O của đường tròn ngoại tiếp tam giác đều ABC là giao điểm của ba đường trung trực (đồng thời là ba đường cao, ba trung tuyến, ba phân giác của tam giác đều ABC).
Ta có: R= OA = AA' =
.
=
.
= √3 (cm).
c) Đường tròn nội tiếp (O;r) tiếp xúc ba cạnh của tam giác đều ABC tại các trung điểm A', B', C' của các cạnh.
r = OA' = AA' =
=
(cm)
d) Vẽ các tiếp tuyến với đường tròn (O;R) tại A,B,C. Ba tiếp tuyến này cắt nhau tại I, J, K. Ta có ∆IJK là tam giác đều ngoại tiếp (O;R).
Đúng 0
Bình luận (0)

a) Vẽ tam giác đều ABC có cạnh bằng 3cm (dùng thước có chia khoảng và compa)
b) Tâm O của đường tròn ngoại tiếp tam giác đều ABC là giao điểm của ba đường trung trực (đồng thời là ba đường cao, ba trung tuyến, ba phân giác của tam giác đều ABC).
Ta có: R= OA = AA' =
.
=
.
= √3 (cm).
c) Đường tròn nội tiếp (O;r) tiếp xúc ba cạnh của tam giác đều ABC tại các trung điểm A', B', C' của các cạnh.
r = OA' = AA' =
=
(cm)
d) Vẽ các tiếp tuyến với đường tròn (O;R) tại A,B,C. Ba tiếp tuyến này cắt nhau tại I, J, K. Ta có ∆IJK là tam giác đều ngoại tiếp (O;R).
Đúng 1
Bình luận (0)
Cho đường tròn (C) ngoại tiếp một tam giác đều ABC có cạnh bằng a, chiều cao AH. Quay đường tròn (C) xung quanh trục AH, ta được một mặt cầu. Thể tích của khối cầu tương ứng là: A.
πa
3
3
54
B.
4
πa
3
9
C.
4...
Đọc tiếp
Cho đường tròn (C) ngoại tiếp một tam giác đều ABC có cạnh bằng a, chiều cao AH. Quay đường tròn (C) xung quanh trục AH, ta được một mặt cầu. Thể tích của khối cầu tương ứng là:
A. πa 3 3 54
B. 4 πa 3 9
C. 4 πa 3 3 27
D. 4 πa 3 3
Chọn C
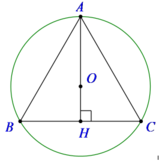
AH là đường cao trong tam giác đều cạnh a nên A H = a 3 2
Gọi O là tâm mặt cầu ngoại tiếp ΔABC, thì O ∈ AH và
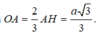
Bán kính mặt cầu được tạo thành khi quay đường tròn (C) quanh trục AH là 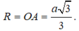 .
.
Vậy thể tích của khối cầu tương ứng là:
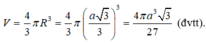
Đúng 0
Bình luận (0)