Ôn tập chương Hình trụ, Hình nón, Hình cầu
Các câu hỏi tương tự
Cho hình vuông ABCD nội tiếp đường tròn tâm O, bán kính R và GEF là tam giác đều nội tiếp đường tròn đó, EF là dây song song với AB (h. 119). Cho hình đó quay xung quanh trục GO. Chứng minh rằng:
a) Bình phương thể tích của hình trụ sinh ra bởi hình vuông bằng tích của thể tích hình cầu sinh ra bởi hình tròn và thể tích hình nón do tam giác đều sinh ra.
b) Bình phương diện tích toàn phần của hình trụ bằng tích của diện tích hình cầu và diện tích toàn phần của hình nón.
Đọc tiếp
Cho hình vuông ABCD nội tiếp đường tròn tâm O, bán kính R và GEF là tam giác đều nội tiếp đường tròn đó, EF là dây song song với AB (h. 119). Cho hình đó quay xung quanh trục GO. Chứng minh rằng:
a) Bình phương thể tích của hình trụ sinh ra bởi hình vuông bằng tích của thể tích hình cầu sinh ra bởi hình tròn và thể tích hình nón do tam giác đều sinh ra.
b) Bình phương diện tích toàn phần của hình trụ bằng tích của diện tích hình cầu và diện tích toàn phần của hình nón.
-0132.jpg)
Với một hình nón có bán kính đường tròn đáy là r (cm) và chiều cao 2r (cm) và một hình cầu bán kính r (cm). Hãy tính :
a) Diện tích mặt cầu, biết diện tích toàn phần của hình nón là \(21,06cm^2\)
b) Thể tích hình nón, biết thể tích hình cầu là \(15,8cm^3\)
Độ dài các cạnh của một tam giác ABC vuông tại A, thỏa mãn các hệ thức sau :
BCAB+2a
ACdfrac{1}{2}left(BC+ABright)
a là một độ dài cho trước
a) Tính theo a, độ dài các cạnh và chiều cao AH của tam giác
b) Tam giác ABC nội tiếp được trong nửa hình tròn tâm O. Tính diện tích của phần thuộc nửa đường tròn nhưng ở ngoài tam giác ssos
c) Cho tam giác ABC quay một vòng quanh cạnh huyền BC. Tính tỉ số diện tích giữa các phần do các dây cung AB và...
Đọc tiếp
Độ dài các cạnh của một tam giác ABC vuông tại A, thỏa mãn các hệ thức sau :
\(BC=AB+2a\)
\(AC=\dfrac{1}{2}\left(BC+AB\right)\)
a là một độ dài cho trước
a) Tính theo a, độ dài các cạnh và chiều cao AH của tam giác
b) Tam giác ABC nội tiếp được trong nửa hình tròn tâm O. Tính diện tích của phần thuộc nửa đường tròn nhưng ở ngoài tam giác ssos
c) Cho tam giác ABC quay một vòng quanh cạnh huyền BC. Tính tỉ số diện tích giữa các phần do các dây cung AB và AC tạo ra
Với nửa hình cầu bán kính r và một hình trụ có bán kính đường tròn đáy và chiều cao đều bằng h
a) Khi r = 12 (cm) và thể tích hai hình bằng nhau thì giá trị h(cm) làm tròn đến chữ số thập phân thứ nhất là bao nhiêu ?
b) Khi h = 12 (cm) và tổng diện tích nửa mặt cầu và diện tích "hình tròn đáy" gấp ba lần diện tích toàn phần của hình trụ thì r (cm) bằng bao nhiêu ?
Hình 120 mô tả một hình cầu được đặt khít vào trong một hình trụ, các kích thước cho trên hình vẽ. Hãy tính:
a) Thể tích hình cầu;
b) Thể tích hình trụ;
c) Hiệu giữa thể tích hình trụ và thể tích hình cầu;
d) Thể tích của một hình nón có bán kính đường tròn đáy là r cm và chiều cao 2r cm;
e) Từ các kết quả a, b, c, d, hãy tìm mối liên hệ giữa chúng.
Đọc tiếp
Hình 120 mô tả một hình cầu được đặt khít vào trong một hình trụ, các kích thước cho trên hình vẽ. Hãy tính:
a) Thể tích hình cầu;
b) Thể tích hình trụ;
c) Hiệu giữa thể tích hình trụ và thể tích hình cầu;
d) Thể tích của một hình nón có bán kính đường tròn đáy là r cm và chiều cao 2r cm;
e) Từ các kết quả a, b, c, d, hãy tìm mối liên hệ giữa chúng.
-0133-1.jpg)
Cho tam giác ABC vuông tại A , đường cao AH
1. Biết AB = 18 cm , AC =24 cm .
a, Tính BC , BH , AH .
b, Tính các góc của tam giác ABC.
2. Kẻ HE vuông góc với AB , HF vuông góc với AC .
Chứng minh AE.EB+À.FC = AH 2
Một hình trụ được "đặt khít" vào bên trong một hình cầu bán kính \(r=12cm\), như hình 112.
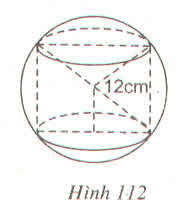
Hãy tính :
a) Diện tích xung quanh của hình trụ, biết chiều cao của hình trụ bằng đường kính đáy của nó
b) Thể tích hình cầu
c) Diện tích mặt cầu
Giúp em với giải với vẽ hình luôn ạ !
1. Cho tam giác ABC có A là một góc vuông. D là một điểm nằm trên cạnh AB. Đường Tròn đường kính BD cắt BC tại E. Các đường thẳng CD;AE lần lượt cắt đường tròn tại các điểm thứ hai F và G.
a) Chứng minh CAFB nội tiếp
b) Chứng minh AB.EDAC.EB
c) Chứng tỏ AC//FG
d) Chứng minh AC;DE;BF đồng quy
2.Cho tam giác ABC vuông tại A, đường cao AH. Gọi O là tâm đường tròn ngoại tiếp tam giác ABC, d là tiếp tuyến của đường tròn tại A, các tiếp tuyến của đường tròn...
Đọc tiếp
Giúp em với giải với vẽ hình luôn ạ !
1. Cho tam giác ABC có A là một góc vuông. D là một điểm nằm trên cạnh AB. Đường Tròn đường kính BD cắt BC tại E. Các đường thẳng CD;AE lần lượt cắt đường tròn tại các điểm thứ hai F và G.
a) Chứng minh CAFB nội tiếp
b) Chứng minh AB.ED=AC.EB
c) Chứng tỏ AC//FG
d) Chứng minh AC;DE;BF đồng quy
2.Cho tam giác ABC vuông tại A, đường cao AH. Gọi O là tâm đường tròn ngoại tiếp tam giác ABC, d là tiếp tuyến của đường tròn tại A, các tiếp tuyến của đường tròn tại B và C lần lượt cắt d theo thứ tự ở D và E.
Chứng minh rằng:
a) Tam giác DOE vuông
b) DE = BD + CE
c) BD . CE = R2 ( R là bán kính của (O) )
d) BC là tiếp tuyến của đường tròn đường kính DE.
cho tam giác ABC(AB<AC) nhọn nội tiếp (O) có BE và CD là 2 đường cao cắt nhau tại H
K là tâm của đường tròn ngoại tiếp tứ giác ADHE. AH cắt đường tròn tại M, cắt BC tại F.
I là trung điểm của BC.
a)C/m: tứ giác KOIM là hình thang cân
b) gọi P, Q là giao điểm của AH và DE; AN và BC
c/m: PQ song song HN





