Cho tam giác ABC. Trên tia đối của ABC lấy điểm D mà AD = AB, trên tia đối của tia AC lấy điểm E mà AE = AC. Gọi M; N lần lượt là các điểm trên BC và ED sao cho CM = EN. Chứng minh ba điểm M; A; N thẳng hàng

Những câu hỏi liên quan
Cho tam giác ABC. Trên tia đối của AB lấy điểm D mà AD=AB, trên tia đối tia AC lấy điểm E mà AE=AC. Gọi M,N lần lượt là các điểm trên BC và ED sao cho CM=EN. C/minh 3 điểm M,A,N thẳng hàng
các bạn giải gấp cho mk vs ạ
Cho tam giác ABC. Trên tia đối của AB lấy điểm D mà AD = AB, trên tia đối tia AC lấy điểm E mà AE = AC. Gọi M; N lần lượt là các điểm trên BC và ED sao cho CM = EN. Chứng minh ba điểm M; A; N thẳng hàng.
Xét \(\Delta ABC\) và \(\Delta ADE\) có:
\(AB=AD\left(gt\right)\)
\(\widehat{BAC}=\widehat{DAE}\) ( tính chất 2 góc đối đỉnh )
\(AC=AE\left(gt\right)\)
Vậy \(\Delta ABC=\) \(\Delta ADE\left(c.g.c\right)\)
\(\Rightarrow\widehat{C}=\widehat{E}\) ( 2 góc tương ứng )
Xét \(\Delta MAC\) và \(\Delta NAE\) có:
\(AC=AE\left(gt\right)\)
\(\widehat{C}=\widehat{E}\left(cmt\right)\)
\(CM=EN\left(gt\right)\)
Vậy \(\Delta MAC=\Delta NAE\left(c.g.c\right)\)
\(\Rightarrow\widehat{MAC}=\widehat{MAE}\) ( 2 góc tương ứng )
Ta có: \(\widehat{MAC}+\widehat{CAD}+\widehat{DAN}=\widehat{NAE}+\widehat{DAN}+\widehat{CAD}\)
\(\Rightarrow\widehat{MAN}=\widehat{CAE}\)
\(\Rightarrow\) 3 điểm \(M,A,N\) thẳng hàng.
Đúng 3
Bình luận (0)
Xét △ABC và △ADE ta có:
⇒ ∠ABC = ∠AED (2 góc tương ứng)
Xét △ACM và △AEN ta có:
⇒ ∠CAM = ∠EAN (2 góc tương ứng)
Mà ∠CAM + ∠CAN = 180o
⇒ ∠EAN + ∠CAN = 180o
⇒ ∠MAN = 180o
⇒ Ba điểm M, A, N thẳng hàng (đcpm).
Đúng 0
Bình luận (0)
Bài 4 (2,5 điểm ): Cho tam giác ABC. Trên tia đối của tia AC lấy điểm D sao cho AD = AC, trên tia đối của tia AB lấy điểm E sao cho AE = AB. Nối D với E.
a) Chứng minh: tam giác ABC=tam giác ADE
b) Chứng minh: BC//DE.
c) Gọi M là trung điểm BC, N là trung điểm DE. Chứng minh ba điểm M, A, N thẳng hàng.
GIÚP EM VỚI Ạ
a) Xét △ ABC và △ AED ta có:
AB = AE ( gt )
\(\widehat{A_1}=\widehat{A_2}\) ( đối đỉnh )
AC = AD ( gt )
⇒ △ ABC = △ AED ( c - g - c )
b ) Vi △ ABC = △ AED ( cmt )
⇒ \(\widehat{D}=\widehat{C}\)
Mà 2 góc ở vị trí so le trong nên
⇒ DE // BC
c) Vì △ ABC = △ AED ( cmt )
⇒ BC = ED = \(\dfrac{1}{2}\)BC = \(\dfrac{1}{2}\) ED
⇒ DN = MC
Xét △ DNA và △ CMA có:
AD = AC ( gt )
\(\widehat{D}=\widehat{C}\)
DN = MC ( cm )
⇒ △ DNA = △ CMA ( c - g - c )
⇒ \(\widehat{DAN}=\widehat{CAM}\)
Do đó: N, A, M thẳng hàng
Đúng 2
Bình luận (1)
Cho \(\Delta ABC\). Trên tia đối của AB lấy điểm D mà AD = AB, trên tia đối của tia AC lấy điểm E mà AE = AC. Gọi M; N lần lượt là các điểm trên BC và ED sao cho CM = EN. Chứng minh ba điểm M; A; N thẳng hàng
Cho tam giác ABC. Trên tia đối của AC lấy D sao cho AD= AC. Trên tia đối của tia AB lấy E sao cho AE= AB. Nối D với E
a) Chứng minh tam giác ABC= tam giác ADE
b) Gọi M là trung điểm của BC, N là trung điểm của DE. Chứng minh AM=AN
a: Xét ΔABC và ΔAED có
AB=AE
\(\widehat{BAC}=\widehat{EAD}\)
AC=AD
Do đó: ΔABC=ΔAED
Đúng 0
Bình luận (0)
Cho \(\Delta ABC\) Trên tia đối của tia AB lấy điểm D mà AD = AB, trên tia đối của tia AC lấy điểm E mà AE = AC. Gọi M; N lần lượt là các điểm trên BC và ED sao cho CM = EN. Chứng minh ba điểm M; A; N thẳng hàng.
Cho tam giác ABC cân tại A. Trên tia đối của tia AB lấy điểm D, trên tia đối của tia AC lấy điểm E sao cho AD = AE. Gọi M là trung điểm của BC. Chứng minh rằng D đối xứng với E qua AM.
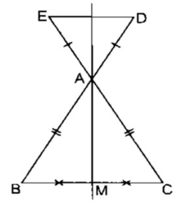
ΔABC cân tại A có AM là đường trung tuyến
⇒ AM là tia phân giác của góc (BAC)
⇒ ∠ (BAM) = ∠ (MAC) (1)
Kéo dài MA cắt DE tai N, ta có:
∠ (BAM) = ∠ (DAN) (đối đỉnh) (2)
∠ (MAC) = ∠ (NAE) (đối đỉnh)(3)
Từ (1), (2) và (3) suy ra: ∠ (DAN) = ∠ (NAE)
∆ ADE cân tại A có AN là tia phân giác
⇒ AN là đường trung trực của DE
hay AM là đường trung trực của DE
Vậy D đối xứng với E qua AM.
Đúng 1
Bình luận (0)
Cho tam giác ABC. Trên tia đối của tia AB lấy điểm D sao cho AD = AC, trên tia đối của tia AC lấy điểm E sao cho AE = AB. Gọi M, N lần lượt là trung điểm của BE và CD.
Chứng minh ba điểm M, A, N thẳng hàng.
\(AD=AC\Rightarrow\)△CAD cân tại A mà AM là trung tuyến.
\(\Rightarrow\)AM cũng là đường phân giác.
\(\Rightarrow\widehat{MAE}=\dfrac{\widehat{BAE}}{2}\left(1\right)\)
\(AE=AB\Rightarrow\)△BAE cân tại A mà AN là trung tuyến.
\(\Rightarrow\)AN cũng là đường phân giác.
\(\Rightarrow\widehat{CAN}=\dfrac{\widehat{CAD}}{2}\left(2\right)\)
Ta có: \(\widehat{BAE}=\widehat{CAD}\) (đối đỉnh), nên từ (1) và (2) suy ra:
\(\widehat{EAM}=\widehat{CAN}\)
Mà \(\widehat{EAM}+\widehat{CAM}=180^0\) (kề bù)
\(\Rightarrow\widehat{CAN}+\widehat{CAM}=180^0\)
\(\Rightarrow\widehat{MAN}=180^0\)
\(\Rightarrow\)M,A,N thẳng hàng.
Đúng 4
Bình luận (0)
cho tam giác ABC . Trên tia đối của tia AB lấy AD = AC , Trên tia đối của tia AC lấy điểm E sao cho AE = AB a) so sánh tam giác ABC và tam giác ADE b) Gọi M và N lần lượt là trung điểm của AC và ED . CMR CM = DN




















