-Áp dụng tính chất sau: Trong một tam giác vuông, nếu có một cạnh góc vuông bằng nửa cạnh huyền thì góc đối diện với cạnh góc vuông đó bằng \(30^o\)

\(\Delta ABC\) vuông tại \(A\) có \(BC=2AB\Rightarrow\widehat{C}=30^o\)

Khi đó: \(\widehat{B}=180^o-\left(\widehat{A}+\widehat{C}\right)=180^o-\left(90^o+30^o\right)=60^o\)

Gọi D là chân đường phân giác kẻ từ B

M là trung điểm AC

+) Theo đề bài BC=2AB => AB=BM=MC (1)

+) \(\widehat{B}=2.\widehat{C}\)

=> \(\widehat{B}_1=\widehat{B_2}=\widehat{C_3}\)(2)

=> Tam giác BDC cân tại D có DM là đường trung tuyến

=> DM vuông BC

+) xét tam giác ADB và tam giác MDB 

có: BD chung

\(\widehat{B}_1=\widehat{B_2}\) (theo 2)

AB=BM (theo 1)

=> Hai tam giác ADB và MDB bằng nhau

=> góc BAD= góc BMD= 90 độ

=> \(\widehat{A}=90^o\)

\(\Rightarrow\widehat{B}+\widehat{C}=180^o-90^o=90^o\Rightarrow3\widehat{C}=90^o\Rightarrow\widehat{C}=30^o\Rightarrow\widehat{B}=2.\widehat{C}=60^o\)

Nguyễn Ling Chi giỏi vl . Mình nghĩ mãi không ra

Ta có: 

\(sinC=\dfrac{AB}{BC}=\dfrac{AB}{2AB}=\dfrac{1}{2}\)

\(\Rightarrow\widehat{C}=30^o\)

Mà: \(\widehat{C}+\widehat{B}=90^o\Rightarrow\widehat{B}=90^o-\widehat{C}=90^o-30^o=60^o\)

Xét tam giác ABC vuông tại A có:

\(sinB=\dfrac{AC}{BC}=\dfrac{4a}{BC}\)

\(\Rightarrow BC=\dfrac{4a}{sinB}=\dfrac{4a}{sin60^o}=\dfrac{4a}{\dfrac{\sqrt{3}}{2}}=\dfrac{8a}{\sqrt{3}}=\dfrac{8\sqrt{3}a}{3}\)

\(\Rightarrow AC=\dfrac{1}{2}BC=\dfrac{1}{2}\cdot\dfrac{8\sqrt{3}}{3}=\dfrac{8\sqrt{3}}{6}a=\dfrac{4\sqrt{3}}{3}a\)

Xét ΔABC vuông tại A có sin C=AB/BC=1/2

nên góc C=30 độ

=>góc B=90-30=60 độ

Xét ΔABC vuông tại A có sin B=AC/BC

=>4a/BC=sin60

=>\(BC=4a:sin60=\dfrac{8}{3}\sqrt{3}\cdot a\)

=>\(AC=\dfrac{1}{2}\cdot BC=\dfrac{4}{3}\cdot\sqrt{3}\cdot a\)

câu hỏi tương tự

tick nha

Kẻ BD là phân giác của góc ABC và Lấy M trên BC sao cho BM=BA

=>BM=1/2BC

Xét ΔBDC có góc DBC=góc DCB

nên ΔBDC cân tại D

mà DM là trung tuyến

nên DM là đường cao

Xét ΔBAD và ΔBMC có

BA=BM

góc ABD=góc MBD

BD chung

Do đó: ΔBAD=ΔBMD

=>góc BMD=góc BAD=90 độ

=>ΔABC vuông tại A

=>góc B+góc C=90 độ

=>góc B=60 độ, góc C=30 độ

trong tam giác ABC vuông tại A có\(sinC=\frac{AB}{BC}=\frac{1}{2}\)

ta có \(sin^2C+cos^2C=1\Rightarrow cos^2C=1-\frac{1}{4}=\frac{3}{4}\) \(\Rightarrow cosC=\frac{\sqrt{3}}{2}\)

lại có \(\frac{sinC}{cosC}=tanC\Rightarrow tanC=\frac{\frac{1}{2}}{\frac{\sqrt{3}}{2}}=\frac{1}{\sqrt{3}}\) 

lại có \(tanC\cdot cotgC=1\Rightarrow cotgC=\frac{1}{\frac{1}{\sqrt{3}}}=\sqrt{3}\)

tim abf: 17.56:2=?

đề thíu

thiếu cái gì?

cái này chỉ là 1 phần trong bài, mấy phần kia biết làm rồi

a: Kẻ DK\(\perp\)BC

Xét ΔBAD vuông tại A và ΔBKD vuông tại K có

BD chung

\(\widehat{ABD}=\widehat{KBD}\)

Do đó: ΔBAD=ΔBKD

=>BA=BK

mà \(BA=\dfrac{1}{2}BC\)

nên \(BK=\dfrac{1}{2}CB\)

=>K là trung điểm của BC

Xét ΔDBC có

DK là đường cao

DK là đường trung tuyến

Do đó: ΔDBC cân tại D

b: ΔDBC cân tại D

=>\(\widehat{DBC}=\widehat{DCB}\)

mà \(\widehat{DBC}=\dfrac{1}{2}\cdot\widehat{ABC}\)

nên \(\widehat{ACB}=\dfrac{1}{2}\cdot\widehat{ABC}\)

ΔABC vuông tại A

=>\(\widehat{ABC}+\widehat{ACB}=90^0\)

=>\(\dfrac{1}{2}\cdot\widehat{ABC}+\widehat{ABC}=90^0\)

=>\(\dfrac{3}{2}\cdot\widehat{ABC}=90^0\)

=>\(\widehat{ABC}=90^0:\dfrac{3}{2}=90^0\cdot\dfrac{2}{3}=60^0\)

\(\widehat{ACB}=\dfrac{1}{2}\cdot\widehat{ABC}=\dfrac{1}{2}\cdot60^0=30^0\)

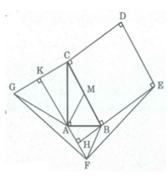
Gọi M là trung điểm của BC, ta có:

AM = MB = 1/2 BC = a (tính chất tam giác vuông)

Suy ra MA = MB = AB = a

Suy ra ∆ AMB đều ⇒  ∠ (ABC) = 60 0

Mặt khác:  ∠ (ABC) +  ∠ (ACB) =  90 0  (tính chất tam giác vuông)

Suy ra:  ∠ (ACB) =  90 0  - ∠ (ABC) =  90 0  –  60 0  =  30 0

Trong tam giác vuông ABC, theo Pi-ta-go, ta có: B C 2 = A B 2 + A C 2

⇒  A C 2 = B C 2 - A B 2 = 4 a 2 - a 2 = 3 a 2 ⇒ AC = a 3

Vậy S A B C  = 1/2 .AB.AC

=  1 2 a . a 3 = a 2 3 2   ( đ v d t )