\(\frac{2}{3}\)số cam còn lại sau lần bán thứ nhất là :

29 + 1 = 30 ( quả )

Số quả cam còn lại sau lần bắn thứ nhất là :

30 : \(\frac{2}{3}\)= 45 ( quả )

Số cam bạn đầu là :

46 : \(\frac{2}{3}\)= 69 ( quả )

   Đáp số : 69 quả cam

sau khi bán 2 đầu đc \(\frac{1}{3}\) còn lại số phần cam còn lại là:

\(1-\frac{1}{3}=\frac{2}{3}\)(số cam)

số cam còn lại là:

29+1=30(quả)

số cam còn lại sau lần 1 bán là:

\(30:\frac{2}{3}=45\)(quả)

sau khi bán lần đầu \(\frac{1}{3}\) số phần cam còn lại là:

\(1-\frac{1}{3}=\frac{2}{3}\)(số cam)

số cam còn lại là:

45+1=46(quả)

ban đầu có số quả cam là:

\(46:\frac{2}{3}=69\)(Quả)

đáp số:69 quả

Help me

b: góc HID+góc HKD=180 độ

=>HIDK nội tiếp

=>góc HIK=góc HDK

=>góc HIK=góc HCB

=>góc HIK=góc HEF

=>EF//IK

a ) 

Xét tứ giác AHBI , ta có : 

\(\widehat{I_2}=90^o\left(gt\right)\)

\(\widehat{H_1}=90^o\left(gt\right)\)

\(\widehat{I_2}+\widehat{H_1}=90^o+90^o=180^o\)

Vay : tứ giác AHBI nội tiếp 

Xét tứ giác AHCK , ta có : 

\(\widehat{K_2}=90^O\left(gt\right)\)

\(\widehat{H_2}=90^o\left(gt\right)\)

\(\widehat{K_2}+\widehat{H_2}=90^o+90^o=180^o\)

Vậy tứ giác AHCK nội tiếp 

a: Xét ΔABD có

AI vừa là đường cao, vừa là trung tuyến

=>ΔABD cân tại A

b: Xét ΔAHI vuông tại H và ΔAKI vuông tại K có

AI chung

góc HAI=góc KAI

=>ΔAHI=ΔAKI

=>HI=KI

c: HI=KI

KI<ID

=>HI<ID

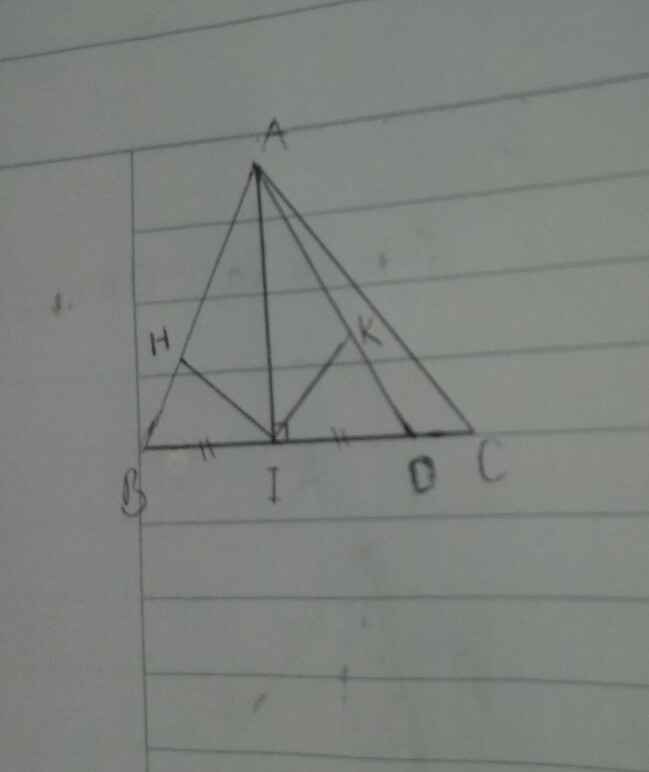
rồi từ câu a) là sai đề nhaaaa em ( ko thể chứng minh đc - do AB < AC < BC) 

Giup mình với. Mình k cho

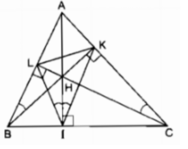
Vì ∆ ABC là tam giác nhọn nên ba đường cao cắt nhau tại điểm H nằm trong tam giác ABC.

Tứ giác AKHL có 

Tứ giác AKHL nội tiếp.

Tứ giác BIHL có 

Tứ giác BIHL nội tiếp.

Tứ giác CIHK có 

Tứ giác CIHK nội tiếp.

Tứ giác ABIK có 

K và I nhìn đoạn AB dưới một góc vuông nên tứ giác ABIK nội tiếp. Tứ giác BCKL có 

K và L nhìn đoạn BC dưới một góc vuông nên tứ giác BCKL nội tiếp.

Tứ giác ACIL có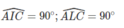 

I và L nhìn đoạn AC dưới một góc vuông nên tứ giác ACIL nội tiếp.