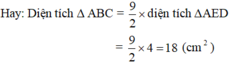cho tam giác ABC. Trên AB lấy điểm D;E sao cho AD = DE = EB. Trên AC lấy điểm H; K sao cho AK = KH = HC. Trên BC lấy điểm M,N sao cho MB = MN = NC. Tính diện tích của lục giác DEMNHK. Biết diện tích tam giác ABC là 270 cm2

Những câu hỏi liên quan
Bài 8: Cho tam giác ABC, AB AC. Trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD CE. Chứng minh: a) Tam giác ADE cân b) ABD ACEBài 9: Cho tam giác ABC, AB AC. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho AD AE. Gọi M là giao điểm của BE và CD. Chứng minh: a) BE CD b) BMD CME. c) AM là tia phân giác của góc BAC. giúp em bài này với ah, em cảm ơn mọi người rất nhiều ( e cần gấp lắm)
Đọc tiếp
Bài 8: Cho tam giác ABC, AB = AC. Trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD = CE. Chứng minh: a) Tam giác ADE cân b) ABD = ACE
Bài 9: Cho tam giác ABC, AB = AC. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho AD = AE. Gọi M là giao điểm của BE và CD. Chứng minh: a) BE = CD b) BMD = CME. c) AM là tia phân giác của góc BAC.
giúp em bài này với ah, em cảm ơn mọi người rất nhiều ( e cần gấp lắm)
Bài 8:
a: Xét ΔABD và ΔACE có
AB=AC
\(\widehat{ABD}=\widehat{ACE}\)
BD=CE
Do đó:ΔABD=ΔACE
Suy ra: AD=AE
b: ta có: ΔABD=ΔACE
nên \(\widehat{ADB}=\widehat{AEC}\)
Đúng 0
Bình luận (0)
Bài 2: Cho tam giác ABC trên tia đối của tia CA lấy điểm D sao cho CD = CA, trên tia đối của tia CB lấy điểm E sao cho CE=CB
a) Chứng minh: tam giác ABC= tam giác DEC
b) Chứng minh: AB //DE
c) Trên cạnh AB lấy điểm M , trên cạnh DE lấy điểm N sao cho AM=DN. Chứng minh:tam giác AMC= tam giác DNC
d) Chứng minh: Ba điểm M, C, N thẳng hàng
a: Xét ΔABC và ΔDEC có
CA=CD
\(\widehat{ACB}=\widehat{DCE}\)
CB=CE
Do đó:ΔACB=ΔDCE
b: Xét tứ giác ABDE có
C là trung điểm của AD
C là trung điểm của BE
Do đó: ABDE là hình bình hành
Suy ra: AB//DE
c: Xét ΔAMC và ΔDNC có
AM=DN
\(\widehat{MAC}=\widehat{NDC}\)
AC=DC
Do đó: ΔAMC=ΔDNC
d: Xét tứ giác AMDN có
AM//DN
AM=DN
Do đó: AMDN là hình bình hành
Suy ra: Hai đường chéo AD và MN cắt nhau tại trung điểm của mỗi đường
mà C là trung điểm của AD
nên C là trung điểm của MN
Đúng 3
Bình luận (0)
https://hoc24.vn/cau-hoi/1cho-tam-giac-abc-co-2-duong-trung-tuyen-bm-va-cn-cat-nhau-tai-g-chung-minh-bm-cn-dfrac32bc2cho-tam-giac-abc-d-la-trung-diem-ac-tren-bd-lay-e-sao-cho-be2ed-f-thuoc-tia-doi-cua-tia.5863553679489
trl câu này hộ mik với chiều nay cần dùng r![]()
Đúng 0
Bình luận (0)
cho hình tam giác ABC .trên BC lấy điểm D sao cho CD 1/3 BC. Trên AB lấy điểm E sao cho BE AB. Nối E với D, biết diện tích hình tam giác BED là 9cm2. Tính diện tích hình tam giác ABC
Đọc tiếp
cho hình tam giác ABC .trên BC lấy điểm D sao cho CD =1/3 BC. Trên AB lấy điểm E sao cho BE = AB. Nối E với D, biết diện tích hình tam giác BED là 9cm2. Tính diện tích hình tam giác ABC
ABD và BDE có Ab=BE , và có chung cạnh BD
=> ABD =BED =9cm2
DC=1/3 BC => DC=1/2 BD
ABD và ACD có DC=1/2 BD và chung đường cao hạ từ đỉnh C
=> ADC = 1/2 ABD = 1/2x9=4,5cm2
=> S. ABC = 9+4,5=13,5cm2
Đúng 1
Bình luận (0)
Cho tam giác ABC. Trên AB lấy điểm D trên AB sao cho AD=1/3AB;
trên AC lấy điểm E sao cho AC= 2 x AE. Cho S.ADE = 10 cm2
. Tính diện tích tam
giác ABC?
Lấy M là trung điểm của DB
=>AD=DM=MB=1/3AB
Xét ΔAMC có AD/AM=AE/AC
nên ΔADE đồng dạng với ΔAMC
=>\(\dfrac{S_{ADE}}{S_{AMC}}=\left(\dfrac{AE}{AC}\right)^2=\dfrac{1}{4}\)
=>\(S_{AMC}=40\left(cm^2\right)\)
AM=2/3AB
=>\(S_{ABC}=\dfrac{3}{2}\cdot S_{AMC}=60\left(cm^2\right)\)
Đúng 0
Bình luận (0)
cho tam giác abc trên cạnh ab lấy điểm d trên cạnh ac lấy điểm e sao cho ab = 5 lần ad , ac =5 lần ae so sanh dtích tam giác ade va d tích tam giac abc
cho tam giác ABC . trên cạnh AB lấy điểm E sao cho AE = 2/3 AB. trên cạnh AC lấy điểm D sao cho AD = 1/3 AC. Nối E với D tính diện tích tam giác ABC ?
cho tam giác abc nhọn có ab < ac. vẽ tia đối của tia ab, trên đó lấy điểm d sao cho ad= ac. vẽ tia đối của tia ac, trên đó lấy điểm e sao cho ae= ab chứng minh tam giác abc bằng tam giác aed
Bài 4 (2,5 điểm ): Cho tam giác ABC. Trên tia đối của tia AC lấy điểm D sao cho AD = AC, trên tia đối của tia AB lấy điểm E sao cho AE = AB. Nối D với E.
a) Chứng minh: tam giác ABC=tam giác ADE
b) Chứng minh: BC//DE.
c) Gọi M là trung điểm BC, N là trung điểm DE. Chứng minh ba điểm M, A, N thẳng hàng.
GIÚP EM VỚI Ạ
a) Xét △ ABC và △ AED ta có:
AB = AE ( gt )
\(\widehat{A_1}=\widehat{A_2}\) ( đối đỉnh )
AC = AD ( gt )
⇒ △ ABC = △ AED ( c - g - c )
b ) Vi △ ABC = △ AED ( cmt )
⇒ \(\widehat{D}=\widehat{C}\)
Mà 2 góc ở vị trí so le trong nên
⇒ DE // BC
c) Vì △ ABC = △ AED ( cmt )
⇒ BC = ED = \(\dfrac{1}{2}\)BC = \(\dfrac{1}{2}\) ED
⇒ DN = MC
Xét △ DNA và △ CMA có:
AD = AC ( gt )
\(\widehat{D}=\widehat{C}\)
DN = MC ( cm )
⇒ △ DNA = △ CMA ( c - g - c )
⇒ \(\widehat{DAN}=\widehat{CAM}\)
Do đó: N, A, M thẳng hàng
Đúng 2
Bình luận (1)
Câu 18 (2,5 điểm). Cho tam giác ABC vuông tại A (AB > AC). Trên tia đối của tia AC lấy điểm D sao cho AD = AB, trên tia đối của tia AB lấy điểm E sao cho AE = AC. Chứng minh:
a)tam giác ABC =tam giác ADE.
b) AEC=ACE= 45 độ
a, Xét ΔABC và ΔADE có :
\(\widehat{EAD}=\widehat{BAC}=90^0\)
\(AB=AD\left(gt\right)\)
\(AE=AC\left(gt\right)\)
\(\Rightarrow\Delta ABC=\Delta ADE\left(2cgv\right)\)
b, Ta có : \(AE=AC\left(gt\right)\)
\(\Rightarrow\) ΔACE cân tại A
\(\Rightarrow\widehat{AEC}=\widehat{ACE}=\dfrac{180^0-\widehat{A}}{2}=\dfrac{180^0-90^0}{2}=45^0\left(đpcm\right)\)
Đúng 1
Bình luận (0)
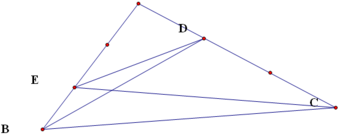
Cho tam giác ABC. Trên cạnh AB lấy điểm E sao cho đoạn AE bằng 2 3 ×AB. Trên cạnh AC lấy điểm D sao cho AD bằng 1 3 ×AC. Nối B với D, nối E với D. Tính diện tích tam giác ABC, biết diện tích tam giác AED bằng 4 c m 2 .