Cho tứ giác ABCD có B+C = 200°;B + D = 180°;C + D=120°.
a) Tính số đo các góc của tứ giác ABCD.
b) Gọi I là giao điểm của các tia phân giác của các góc BAD và ABC của tứ giác. Chứng minh AIB = C+D/2
Cho tứ giác ABCD biết:
\(\widehat{B}+\widehat{C}=200^o;\widehat{B}+\widehat{D}=180^o;\widehat{C}+\widehat{D}=120^o\)
Tính các góc của tứ giác ABCD
góc C-góc D=200-180=20 độ
góc C+góc D=120 độ
=>góc C=(20+120)/2=70 độ và góc D=120-70=50 độ
góc B=200-70=130 độ
góc A=180-70=110 độ
1 Cho tứ giác ABCD, trong đó có A +B = 140°. Tổng C + D = A. 220° B. 200° C. 160° D. 150°
Cho hình tứ giác ABCD có góc B + góc C=200 độ, góc B+ góc D = 180 độ, góc C + góc D =120 độ.Tính các góc của tứ giác.Giúp mình với.
cho tứ giác ABCD có B+C = 200 độ;B+D=180 độ;C+D= 120 độ
a) tính các góc của tứ giác
b) Các tia phan giác a và b cat nhau tại I .cmr góc aib=c+d/2
Tứ giác ABCD có C=700,D=800,A-B=200.Tính số đo các góc A và B
Xét tứ giác ABCD có
\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^0\)
=>\(\widehat{A}+\widehat{B}=360^0-70^0-80^0=210^0\)
mà \(\widehat{A}-\widehat{B}=20^0\)
nên \(\widehat{A}=\dfrac{210^0+20^0}{2}=115^0\)
=>\(\widehat{B}=115^0-20^0=95^0\)
Cho tứ giác ABCD có tổng số đo góc ngoài tại hai đỉnh B và C là 200 ° . Tổng số đo các góc ngoài tại 2 đỉnh A, C là:
A. 160 °
B. 260 °
C. 180 °
D. 100 °
Đáp án cần chọn là: A
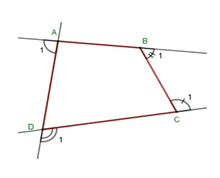
Gọi góc ngoài tại 4 đỉnh A, B, C, D của tứ giác ABCD lần lượt là A 1 ^ ; B 1 ^ ; C 1 ^ ; D 1 ^ .
Khi đó ta có :
A ^ + A 1 ^ = 180 ° ⇒ A 1 ^ = 180 ° - A ^ ; B ^ + B 1 ^ = 180 ° ⇒ B 1 ^ = 180 ° - B ^ ; C ^ + C 1 ^ = 180 ° ⇒ C 1 ^ = 180 ° - C ^ ; D ^ + D 1 ^ = 180 ° ⇒ D 1 ^ = 180 ° - D ^ ;
Suy ra
A 1 ^ + B 1 ^ + C 1 ^ + D 1 ^ = 180 ° - A ^ + 180 ° - B ^ + 180 ° - C ^ + 180 ° - D ^ = 720 ° - A ^ + B ^ + C ^ + D ^ = 720 ° - 360 ° = 360 °
Vậy tổng số đo các góc ngoài tại 4 đỉnh A, B, C, D là 360 ° .
Mà tổng số đo góc ngoài tại hai đỉnh B, C bằng 200 ° nên tổng số đo góc ngoài tại hai đỉnh A, D bằng 360 ° - 200 ° = 160 °
Bài 4: Tứ giác ABCD có 𝐴̂ = 600; 𝐵̂=900. Tính góc C, góc D và góc ngoài của tứ giác tại đỉnh C nếu :
a) GÓC C− GÓC D=200 b) C= 3/4 GÓC D
a: Xét tứ giác ABCD có
\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^0\)
\(\Leftrightarrow\widehat{C}+\widehat{D}=210^0\)
mà \(\widehat{C}-\widehat{D}=20^0\)
nên \(2\cdot\widehat{C}=230^0\)
\(\Leftrightarrow\widehat{C}=115^0\)
\(\Leftrightarrow\widehat{D}=95^0\)
Số đo góc ngoài tại đỉnh C là: \(180^0-115^0=65^0\)
b: Ta có: \(\widehat{C}+\widehat{D}=210^0\)
\(\Leftrightarrow\widehat{D}\cdot\dfrac{7}{4}=210^0\)
\(\Leftrightarrow\widehat{D}=120^0\)
\(\Leftrightarrow\widehat{C}=90^0\)
Số đo góc ngoài tại đỉnh C là: \(180^0-90^0=90^0\)
BÀI 1 : CHO TỨ GIÁC ABCD CÓ : \(\widehat{A}+\widehat{B}=200^{^0};\widehat{B}+\widehat{C}=218^0;\widehat{C}+\widehat{D}=160^0\) TÍNH \(\widehat{C}\)VÀ \(\widehat{D}\)
BÀI 2 : CHO TỨ GIÁC ABCD CÓ \(\widehat{B}=80^0;\widehat{D}=120^0\)GÓC NGOÀI ĐỈNH C BẰNG 1300 . TÍNH GÓC A CỦA TỨ GIÁC
BÀI 3 : TỨ GIÁC ABCD CÓ \(\widehat{A}=57^0;\widehat{C}=110^0;\widehat{D}=75^0\).TÍNH GÓC NGOÀI TẠI ĐỈNH B