trong mặt phẳng toạ độ Oxy, cho tam giác ABC có A(5;3), B(2;-1), C(-1;5)
a) Chứng minh A,B,C là 3 đỉnh của một tam giác
b) tìm toạ độ điểm M sao cho OM=2AB-3AC
c) tìm toạ độ điểm H là trực tâm tam giác ABC
Trong mặt phẳng toạ độ Oxy, cho tam giác ABC có A(-3,0); B(3,0); và C(2,6). Tìm toạ độ trục tâm H của tam giác ABC
Gọi \(H\left(x;y\right)\) là trực tâm tam giác
\(\Rightarrow\overrightarrow{AH}=\left(x+3;y\right)\) ; \(\overrightarrow{BH}=\left(x-3;y\right)\); \(\overrightarrow{BC}=\left(-1;6\right)\) ; \(\overrightarrow{AC}=\left(5;6\right)\)
Do H là trực tâm tam giác \(\Rightarrow\left\{{}\begin{matrix}AH\perp BC\\BH\perp AC\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AH}.\overrightarrow{BC}=0\\\overrightarrow{BH}.\overrightarrow{AC}=0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}-\left(x+3\right)+6y=0\\5\left(x-3\right)+6y=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}-x+6y=3\\5x+6y=15\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=2\\y=\dfrac{5}{6}\\\end{matrix}\right.\) \(\Rightarrow H\left(2;\dfrac{5}{6}\right)\)
Trong mặt phẳng toạ độ Oxy cho tam giác ABC có A(1;1) , B(2;-1) , C(3;3) . Toạ độ điểm E để tứ giác ABCE là hình bình hành là
Gọi E(x;y) \(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AB}=\left(1;-2\right)\\\overrightarrow{EC}=\left(3-x;3-y\right)\end{matrix}\right.\)
Tứ giác ABCE là hbh khi \(\overrightarrow{AB}=\overrightarrow{EC}\)
\(\Leftrightarrow\left\{{}\begin{matrix}3-x=1\\3-y=-2\end{matrix}\right.\) \(\Rightarrow E\left(2;5\right)\)
Trong mặt phẳng với hệ toạ độ Oxy cho tam giác ABC. Hai điểm M 4 ; - 1 , N 0 ; - 5 lần lượt thuộc AB, AC và phương trình đường phân giác trong góc A là x - 3 y + 5 = 0 , trọng tâm của tam giác ABC là G. Tìm toạ độ các đỉnh của tam giác ABC
A. A 1 ; 2 , B - 2 ; 5 , C - 1 ; 12
B. A 1 ; 2 , B - 2 ; 5 , C 0 ; 1
C. A 1 ; 0 , B - 2 ; 5 , C - 1 ; 12
D. A 1 ; 2 , B - 1 ; 5 , C - 1 ; 12
Đáp án A
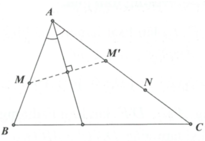
Phân tích.
- Ta thấy A thuộc đường phân giác trong góc A: x - 3 y + 5 = 0 giờ chỉ cần viết được phương trình AC là tìm được A.
- Trên AC đã có một điểm N, cần tìm thêm một điểm nữa. Chú ý khi lấy M’ đối xứng với M qua phân giác trong ta có M’ thuộc cạnh AC.
- Tìm M’ viết được phương trình AC từ đó suy ra A. Có A, M viết được phương trình AB.
- Gọi B, C và tham số hóa dựa vào B thuộc AB, C thuộc AC. Áp dụng công thức trọng tâm sẽ tìm ra được tọa độ B, C.
Hướng dẫn giải.
Gọi M ' ∈ A C là điểm đối xứng của M qua phân giác trong góc A, gọi I là giao điểm của MM' với phân giác trong góc A → I là trung điểm MM’.
Phương trình MM’ là: 3 x + y - 11 = 0
Toạ độ điểm I là nghiệm của hệ:
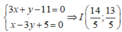
M’ đối xứng với M qua
![]()
Đường thẳng AC qua N và M’ nên có phương trình:
![]()
Tọa độ A là nghiệm của hệ:
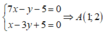
Đường thẳng AB đi qua A, M nên có phương trình:
x + y - 3 = 0
Gọi
![]()
Do G là trọng tâm tam giác ABC nên ta có:
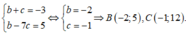
Vậy tọa độ các đỉnh của tam giác ABC là:
![]()
Trong mặt phẳng toạ độ Oxy, cho 2 điểm A(1,2) và B(-3,1). Tìm toạ độ điểm C thuộc trục tung sao cho tam giác ABC vuông tại A. Tính diện tích tam giác ABC
Do C thuộc trục tung nên tọa độ có dạng \(C\left(0;c\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AB}=\left(-4;-1\right)\\\overrightarrow{AC}=\left(-1;c-2\right)\end{matrix}\right.\)
Do tam giác ABC vuông tại A \(\Rightarrow\overrightarrow{AB}.\overrightarrow{AC}=0\)
\(\Rightarrow4-\left(c-2\right)=0\Rightarrow c=6\)
\(\Rightarrow C\left(0;6\right)\)
\(\Rightarrow\overrightarrow{AC}=\left(-1;4\right)\Rightarrow\left\{{}\begin{matrix}AB=\sqrt{\left(-4\right)^2+\left(-1\right)^2}=\sqrt{17}\\AC=\sqrt{\left(-1\right)^2+4^2}=\sqrt{17}\end{matrix}\right.\)
\(\Rightarrow S_{ABC}=\dfrac{1}{2}AB.AC=\dfrac{17}{2}\)
Trong mặt phẳng toạ độ Oxy, cho tam giác ABC có A(6,0); B(3,1); C(-1,-1).Tính số đo góc B của tam giác đã cho
\(\left\{{}\begin{matrix}\overrightarrow{BA}=\left(3;-1\right)\\\overrightarrow{BC}=\left(-4;-2\right)\end{matrix}\right.\)
\(\Rightarrow cos\widehat{ABC}=cos\left(\overrightarrow{BA};\overrightarrow{BC}\right)=\dfrac{3.\left(-4\right)+1.2}{\sqrt{3^2+1^2}.\sqrt{\left(-4\right)^2+\left(-2\right)^2}}=-\dfrac{\sqrt{2}}{2}\)
\(\Rightarrow\widehat{ABC}=135^0\)
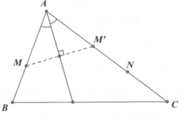
Trong mặt phẳng với hệ toạ độ Oxy cho tam giác ABC. Hai điểm M(4;-1),N(0;-5) lần lượt thuộc AB, AC và phương trình đường phân giác trong góc A là x- 3y+5 = 0, trọng tâm của tam giác ABC là G. Tìm toạ độ các đỉnh của tam giác ABC.
![]()
![]()
![]()
![]()
Chọn A
Phân tích.
- Ta thấy A thuộc đường phân giác trong góc A:x-3y+5=0 , giờ chỉ cần viết được phương trình AC là tìm được A.
- Trên AC đã có một điểm N, cần tìm thêm một điểm nữa. Chú ý khi lấy M’ đối xứng với M qua phân giác trong ta có M’ thuộc cạnh AC.
- Tìm M’ viết được phương trình AC từ đó suy ra A. Có A, M viết được phương trình AB.
- Gọi B, C và tham số hóa dựa vào B thuộc AB, C thuộc AC. Áp dụng công thức trọng tâm sẽ tìm ra được tọa độ B, C.



Trên mặt phẳng toạ độ Oxy cho 3 điểm. điểm A có toạ độ 1;4, điểm B có toạ độ -3;-4, điểm C có toạ độ 1;0. Tính diện tích của tam giác ABC
Giúp em với ạ em cảm ơn!
Trong mặt phẳng toạ độ Oxy, cho tam giác ABC có A(6;-1) B(-1;2) C(2;5)
a) tính độ dài 3 cạnh vf số đo 3 góc của tam giác ABC
b)Tính chu vi và diện tích của tam giác ABC
c) Tìm toạ độ trực tâm , trọng tâm tam giác ABC.
Gợi ý thôi nhé.
a) Có \(AB=\sqrt{\left(x_B-x_A\right)^2+\left(y_B-y_A\right)^2}=\sqrt{\left(\left(-1\right)-6\right)^2+\left(2-\left(-1\right)\right)^2}=\sqrt{58}\)
Tương tự như vậy, ta tính được AC, BC.
Tính góc: Dùng \(\cos A=\dfrac{AB^2+AC^2-BC^2}{2AB.AC}\)
b) Chu vi thì bạn lấy 3 cạnh cộng lại.
Diện tích: Dùng \(S_{ABC}=\dfrac{1}{2}AB.AC.\sin A\)
c) Gọi \(H\left(x_H,y_H\right)\) là trực tâm thì \(\left\{{}\begin{matrix}AH\perp BC\\BH\perp AC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\overrightarrow{AH}.\overrightarrow{BC}=0\\\overrightarrow{BH}.\overrightarrow{AC}=0\end{matrix}\right.\)
Sau đó dùng: \(\overrightarrow{u}\left(x_1,y_1\right);\overrightarrow{v}\left(x_2,y_2\right)\) thì \(\overrightarrow{u}.\overrightarrow{v}=x_1x_2+y_1y_2\) để lập hệ phương trình tìm \(x_H,y_H\)
Trọng tâm: Gọi \(G\left(x_G,y_G\right)\) là trọng tâm và M là trung điểm BC. Dùng \(\left\{{}\begin{matrix}x_M=\dfrac{x_B+x_C}{2}\\y_M=\dfrac{y_B+y_C}{2}\end{matrix}\right.\) để tìm tọa độ M.
Dùng \(\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AM}\) để lập hpt tìm tọa độ G.
Trong mặt phẳng toạ độ Oxy, cho 2 điểm A(-2,4) và B(8,4). Tìm toạ độ điểm C thuộc trục hoành sao cho tam giác ABC vuông tại C
Do C thuôc trục hoành nên tọa độ có dạng \(C\left(c;0\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AC}=\left(c+2;-4\right)\\\overrightarrow{BC}=\left(c-8;-4\right)\end{matrix}\right.\)
Do tam giác ABC vuông tại C \(\Rightarrow\overrightarrow{AC}.\overrightarrow{BC}=0\)
\(\Rightarrow\left(c+2\right)\left(c-8\right)+16=0\)
\(\Rightarrow c^2-6c=0\Rightarrow\left[{}\begin{matrix}c=0\\c=6\end{matrix}\right.\)
Vậy có 2 điểm C thỏa mãn là \(C\left(0;0\right)\) và \(C\left(6;0\right)\)
Trong mặt phẳng hệ toạ độ Oxy. Cho tam giác ABC có đỉnh C(-5,-6) và đường cao AH: x+2y+1=0, đường trung tuyến BM : 8x-y+4=0. Tìm toạ độ các đỉnh A,B Các bạn giúp mình nhanh với
\(M=\left(m;8m+4\right)\) là trung điểm AC.
\(\Rightarrow A=\left(2m+5;16m+14\right)\)
Mà \(A\in AH\Rightarrow2m+5+2\left(16m+14\right)+1=0\)
\(\Rightarrow m=-1\)
\(\Rightarrow A=\left(3;-2\right)\)
Đường thẳng BC đi qua \(C=\left(-5;-6\right)\) và vuông góc AH có phương trình:
\(2x-y+4=0\)
B có tọa độ là nghiệm của hệ \(\left\{{}\begin{matrix}8x-y+4=0\\2x-y+4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=4\end{matrix}\right.\Rightarrow B=\left(0;4\right)\)