Cho hai điểm M(2;3) và N(-2;5). Đường thẳng MN có một vectơ chỉ phương là
A. u → = ( 4 ; 2 )
B. u → = ( 4 ; - 2 )
C. u → = ( - 4 ; - 2 )
D. u → = ( - 2 ; 4 )
Vẽ hai đường thẳng a, b và hai điểm M, N sao cho M ∈ a, M ∈ b, N ∈ b. Vẽ điểm P sao cho 2 điểm N và P nằm khác phía so với điểm M. Vẽ 2 điểm K và F thuộc đường thẳng a sao cho 2 điểm K và F cùng phía so với điểm M.
Cho hai tia Ox và Oy đối nhau. Trên tia Ox lấy hai điểm M và N sao cho OM = 2 cm, ON = 3cm. Trên tia Oy, lấy điểm O sao cho OP = 2 cm.
Trong ba điểm O, M, N điểm nào nằm giữa hai điểm còn lại? Vì sao?
cho đoạn thẳng AB = 8 cm và điểm M nằm giữa hai điểm A và B sao cho AM = 3 cm.Biết điểm E nằm giữa hai điểm A và M sao cho AE = 1 cm,điểm F nằm giữa hai điểm M và B sao cho FB = 2 cm a) Tính đọ dài đoạn thẳng MB , b) nêu tên những điểm nằm cùng phía với điểm F, c) cặp 2 điểm nào nhận điểm M nằm giữa d) điểm E là mút chung của những đoạn thằng nào, e) Tính độ dài đoạn EM và EF
Trong đề cương toán 6 Trường THCS Linh Đàm bè
Cho góc bẹt xOy, trên tia Ox lấy điểm A sao cho OA = 2 cm; trên tia Oy lấy hai điểm M và B sao cho OM = 1 cm; OB = 4 cm.
a. Chứng tỏ: Điểm M nằm giữa hai điểm O và B; Điểm M là trung điểm của đoạn thẳng AB.
b. Từ O kẻ hai tia Ot và Oz sao cho tOy=130o, zOy=30o . Tính số đo tOz
a) Trên tia Oy ta có OM = 1 cm < OB = 4 cm
Vậy M là điểm nằm giữa O và B
Do M nằm giữa O và B ta có: OM + MB = OB
MB = OB – OM = 4 – 1 = 3
Do A thuộc tia Ox , M thuộc tia Oy nên O nằm giữa hai điểm A và M
suy ra OM + OA = MA
MA = 2 + 1 = 3 cm
Mặt khác do A, B nằm trên hai tia đối nhau, M nằm giữa O và B nên M nằm giữa A và B.
Vậy M là trung điểm của AB
b) TH1: Tia Ot và tia Oz trên cùng một nửa mặt phẳng.
Do \(\widehat{\text{yOt}}\) = 130o , \(\widehat{\text{yOz}}\) = 30o suy ra tia Oz nằm giữa hai tia Ot và Oy.
Ta có \(\widehat{\text{tOy}}\) = \(\widehat{\text{tOy}}\) – \(\widehat{\text{yOz}}\) = 130o – 30o = 100o
TH2: Tia Ot và tia Oz không nằm trên cùng một nữa mặt phẳng bờ là xy
Suy ra tia Oy nằm giữa hai tia Ot và Oz
Ta có \(\widehat{tOz}\) = \(\widehat{\text{tOy}}\) + \(\widehat{yOz}\) = 130o + 30o = 160o
a) Trên tia Oy ta có OM = 1 cm < OB = 4 cm
Vậy M là điểm nằm giữa O và B
Do M nằm giữa O và B ta có: OM + MB = OB
MB = OB – OM = 4 – 1 = 3
Do A thuộc tia Ox , M thuộc tia Oy nên O nằm giữa hai điểm A và M
suy ra OM + OA = MA
MA = 2 + 1 = 3 cm
Mặt khác do A, B nằm trên hai tia đối nhau, M nằm giữa O và B nên M nằm giữa A và B.
Vậy M là trung điểm của AB
b) TH1: Tia Ot và tia Oz trên cùng một nửa mặt phẳng.
Do ˆyOtyOt^ = 130o , ˆyOzyOz^ = 30o suy ra tia Oz nằm giữa hai tia Ot và Oy.
Ta có ˆtOytOy^ = ˆtOytOy^ – ˆyOzyOz^ = 130o – 30o = 100o
TH2: Tia Ot và tia Oz không nằm trên cùng một nữa mặt phẳng bờ là xy
Suy ra tia Oy nằm giữa hai tia Ot và Oz
Ta có ˆtOztOz^ = ˆtOytOy^ + ˆyOzyOz^ = 130o + 30o = 160o
1)Cho 4 điểm A,B,M,N sao cho điểm M nằm giữa 2 điểm A và B;điểm B nằm giữa 2 điểm M và N.Chứng tỏ rằng hai đường thẳng AB và MN trùng nhau.
Cho hai điểm A(2; 4) và M(5 ; 7). Tìm toạ độ điểm B sao cho M là trung điểm đoạn thẳng AB.
Giả sử B có tọa độ: \(B\left( {{x_B},{y_B}} \right)\)
Do M là trung điểm của đoạn thẳng AB nên: \(\left\{ \begin{array}{l}{x_M} = \frac{{{x_A} + {x_B}}}{2}\\{y_M} = \frac{{{y_A} + {y_B}}}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_B} = 2{x_M} - {x_A}\\{y_B} = 2{y_M} - {y_A}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_B} = 2.5 - 2 = 8\\{y_B} = 2.7 - 4 = 10\end{array} \right.\)
Vậy tọa độ điểm B là: \(B\left( {8;10} \right)\)
Giả sử B có tọa độ: \(B\left(x_B,y_B\right)\)
Do M là trung điểm của đoạn thẳng AB nên:
\(\left\{{}\begin{matrix}x_M=\dfrac{x_A+x_B}{2}\\y_M=\dfrac{y_A+y_B}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_B=2x_M-x_A\\y_B=2y_M-y_A\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_B=2.5-2=8\\y_{B=}=2.7-4=10\end{matrix}\right.\)
Cho hai điểm A(-3; 2), B(4; 3). Biết có 2 điểm M trên trục Ox sao cho tam giác MAB vuông tại M. Tính tổng hoành độ 2 điểm đó.
A. -1
B. 0
C. 1
D. 2
Chọn C.
Điểm M ∈ Ox ⇒ M(x; 0).
Khi đó ![]()
ΔMAB vuông tại M nên ![]()
Hay (–3 – x)(4 – x) + 2.3 = 0
⇔ –12 + 3x – 4x + x2 + 6 = 0
⇔ x2 – x – 6 = 0 ⇔ 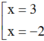 .
.
Vậy: M1(3; 0), M2(-2; 0) và tổng hoành độ của chúng là : 3 + (-2) = 1.
Bài 1. Cho đoạn thẳng AB = 5cm .Trên đoạn thẳng Ab lấy 2 điểm M,N sao cho AM = BN = 3cm.
a)Tính độ dài MB và chứng tỏ điểm M nằm giữa hai điểm N và B.
b) diểm M nằm giữa hai điểm M và A
Bài 2. Cho MN =6cm .Trên đoạn thẳng MN ,vẽ A sao cho MA =1/3 MN ,vẽ B sao cho NB =1/3 MN.
a) Điểm A có nằm giữa hai điểm M và n không ? Vì sao ?
b) Chứng tỏ rằng diểm B nằm giữa hai điểm M,N.
c) Trong ba điểm A, B ,N diểm nào nằm giữa hai điểm còn lại ?
Bài 1 :
a, độ dài MB = AB - NB
suy ra : 5 - 3 = 2 cm
điểm m nằm giữa N và B vì NB - NM = MB và NM +MB = NB
b, Điểm N nằm giữa M và A vì AN +NM = AM VÀ AM - AN = NM
Bài 2
a, có vì MA +AN = MN VÀ MN - MA = AN
b, vì MB +BN = MN nên B nằm giữa MN
c, Trong ba điểm thì B nằm giữa hai điểm còn lại
ĐÂY LÀ CÁCH CỦA MÌNH NẾU SAI THÌ THÔI NHÉ HIHI
1. Cho hai điểm M (-1;3) và N (4;1). Tìm điểm K' trên trục hoành M,N,K thẳng hàng
2. Cho hai điểm M (-1;-3) và N (2;2). Tìm điểm P trên trục hoành và điểm Q trên trục tung sao cho M,N,P,Q thẳng hàng
3. Tìm a,b biết đường thẳng y = ax + b đi qua điểm M (0;-3) và cắt đường thẳng y = -x+3 tại điểm N có hoành độ bằng 2
1. Cho hai điểm M (-1;3) và N (4;1). Tìm điểm K' trên trục hoành M,N,K thẳng hàng
2. Cho hai điểm M (-1;-3) và N (2;2). Tìm điểm P trên trục hoành và điểm Q trên trục tung sao cho M,N,P,Q thẳng hàng
3. Tìm a,b biết đường thẳng y = ax + b đi qua điểm M (0;-3) và cắt đường thẳng y = -x+3 tại điểm N có hoành độ bằng 2