chứng minh rằng với mọi số tự nhiên n,các số sau là các số nguyên tố cùng nhau
a) n+1;n+2
b) 3n+10;3n+9
(Nếu ƯCLN(a,b)= thì hai số a,b được gọi là hai số nguyên tố cùng nhau)
*giúp tui vớiiiiiiiiiii*
Chứng tỏ rằng với mọi số tự nhiên n, các số sau đây là hai số nguyên tố cùng nhau
A) n +2 và n +3
B) 2n +3 và 3n +5
Lời giải:
a. Gọi $d$ là ƯCLN $(n+2, n+3)$
$\Rightarrow n+2\vdots d, n+3\vdots d$
$\Rightarrow (n+3)-(n+2)\vdots d$ hay $1\vdots d$
$\Rightarrow d=1$
Vậy $ƯCLN(n+2, n+3)=1$ hay $n+2, n+3$ nguyên tố cùng nhau.
b.
Gọi $d$ là ƯCLN $(2n+3, 3n+5)$
$\Rightarrow 2n+3\vdots d$ và $3b+5\vdots d$
$\Rightarrow 2(3n+5)-3(2n+3)\vdots d$
$\Rightarrow 1\vdots d\Rightarrow d=1$
Vậy $(2n+3,3n+5)=1$ nên 2 số này nguyên tố cùng nhau.
a) chứng minh rằng khi nla số tự nhiên khác 0 thì n+1 là 2 số nguyên tố cùng nhau.
b)chứng minh rằng với mọi số tự nhiên n thì các số sau là nguyên tố cùng nhau :2n+3 va 4n+8
e có 2 chia hết cho d; 2n+3 lẻ nên (2n+3,4n+8)=1
còn n+1-n=1 nên (n,n+1)=1
1.Chứng tỏ rằng hai số lẻ liên tiếp là hai số nguyên tố cùng nhau
2.Chứng minh rằng với mọi số tự nhiên , các số sau là các số nguyên tố cùng nhau.
a) n+1 và n+2 b)2n+2 và 2n+3
c)2n+1 và n+1 d)n+1 và 3n+4
Bài 1: Gọi hai số lẻ liên tiếp là $2k+1$ và $2k+3$ với $k$ tự nhiên.
Gọi $d=ƯCLN(2k+1, 2k+3)$
$\Rightarrow 2k+1\vdots d; 2k+3\vdots d$
$\Rightarrow (2k+3)-(2k+1)\vdots d$
$\Rightarrow 2\vdots d\Rightarrow d=1$ hoặc $d=2$
Nếu $d=2$ thì $2k+1\vdots 2$ (vô lý vì $2k+1$ là số lẻ)
$\Rightarrow d=1$
Vậy $2k+1,2k+3$ nguyên tố cùng nhau.
Ta có đpcm.
Bài 2:
a. Gọi $d=ƯCLN(n+1, n+2)$
$\Rightarrow n+1\vdots d; n+2\vdots d$
$\Rightarrow (n+2)-(n+1)\vdots d$
$\Rightarrow 1\vdots d\Rightarrow d=1$
Vậy $(n+1, n+2)=1$ nên 2 số này nguyên tố cùng nhau.
b.
Gọi $d=ƯCLN(2n+2, 2n+3)$
$\Rightarrow 2n+2\vdots d; 2n+3\vdots d$
$\Rightarrow (2n+3)-(2n+2)\vdots d$ hay $1\vdots d$
$\Rightarrow d=1$.
Vậy $(2n+2, 2n+3)=1$ nên 2 số này nguyên tố cùng nhau.
Bài 2:
c.
Gọi $d=ƯCLN(2n+1, n+1)$
$\Rightarrow 2n+1\vdots d; n+1\vdots d$
$\Rightarrow 2(n+1)-(2n+1)\vdots d$
$\Rightarrow 1\vdots d\Rightarrow d=1$
Vậy $ƯCLN(2n+1, n+1)=1$ nên 2 số này nguyên tố cùng nhau.
d.
Gọi $d=ƯCLN(n+1, 3n+4)$
$\Rightarrow n+1\vdots d; 3n+4\vdots d$
$\Rightarrow 3n+4-3(n+1)\vdots d$
$\Rightarrow 1\vdots d\Rightarrow d=1$
Vậy $ƯCLN(n+1, 3n+4)=1$
$\Rightarrow$ 2 số này nguyên tố cùng nhau.
1.Chứng minh rằng: Với mọi số tự nhiên các số sau là các số nguyên tố cùng nhau.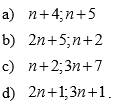
2.Tìm các số tự nhiên để các số sau nguyên tố cùng nhau. 
1:
a: Gọi d=ƯCLN(n+5;n+4)
=>\(\left\{{}\begin{matrix}n+5⋮d\\n+4⋮d\end{matrix}\right.\)
=>\(n+5-n-4⋮d\)
=>\(1⋮d\)
=>d=1
=>n+4 và n+5 là hai số nguyên tố cùng nhau
b: Gọi d=ƯCLN(2n+5;n+2)
=>\(\left\{{}\begin{matrix}2n+5⋮d\\n+2⋮d\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2n+5⋮d\\2n+4⋮d\end{matrix}\right.\)
=>\(2n+5-2n-4⋮d\)
=>\(1⋮d\)
=>d=1
=>2n+5 và n+2 là hai số nguyên tố cùng nhau
c: Gọi d=ƯCLN(3n+7;n+2)
=>\(\left\{{}\begin{matrix}3n+7⋮d\\n+2⋮d\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3n+7⋮d\\3n+6⋮d\end{matrix}\right.\)
=>\(3n+7-3n-6⋮d\)
=>\(1⋮d\)
=>d=1
=>3n+7 và n+2 là hai số nguyên tố cùng nhau
d: Gọi d=ƯCLN(2n+1;3n+1)
=>\(\left\{{}\begin{matrix}2n+1⋮d\\3n+1⋮d\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}6n+3⋮d\\6n+2⋮d\end{matrix}\right.\)
=>\(6n+3-6n-2⋮d\)
=>\(1⋮d\)
=>d=1
=>2n+1 và 3n+1 là hai số nguyên tố cùng nhau
a) Gọi d là ƯCLN của n + 4 và n + 5
⇒ n + 4 ⋮ d và n + 5 ⋮ d
⇒ (n + 5 - n - 4) ⋮ d
⇒ 1 ⋮ d
⇒ d = 1
Vậy n + 4 và n + 5 luôn là cặp SNT cùng nhau
b) Gọi d là ƯCLN của 2n + 5 và n + 2
⇒ 2n + 5 ⋮ d và n + 2 ⋮ d
⇒ 2n + 5 ⋮ d và 2(n + 2) ⋮ d
⇒ (2n + 5 - 2n - 4) ⋮ d
⇒ 1 ⋮ d
⇒ d = 1
Vậy 2n + 5 và n + 2 luôn là cặp SNT cùng nhau
c) Gọi d là ƯCLN của n + 2 và 3n + 7
⇒ n + 2 ⋮ d và 3n + 7 ⋮ d
⇒ 3(n + 2) ⋮ d và 3n + 7 ⋮ d
⇒ (3n + 7 - 3n - 6) ⋮ d
⇒ 1 ⋮ d
⇒ d = 1
Vậy n + 2 và 3n + 7 luôn là cặp SNT cùng nhau
d) Gọi d là ƯCLN của 2n + 1 và 3n + 1
⇒ 2n + 1 ⋮ d và 3n + 1 ⋮ d
⇒ 3(2n + 1) ⋮ d và 2(3n + 1) ⋮ d
⇒ (6n + 3 - 6n - 2) ⋮ d
⇒ 1 ⋮ d
⇒ d = 1
Vậy 2n + 1 và 3n + 1 luôn là cặp SNT cùng nhau
1 chứng minh rằng với mọi số tự nhiên n, các số sau nguyên tố cùng nhau
n+1 và 2n+1
b: Gọi d=ƯCLN(2n+1;n+1)
=>2n+1 chia hết cho d và n+1 chia hết cho d
=>2n+2 chia hết cho d và 2n+1 chia hết cho d
=>2n+2-2n-1 chia hết cho d
=>1 chia hết cho d
=>d=1
=>ĐPCM
Bài 1: Chứng tỏ rằng với mọi số tự nhiên n thì hai số nguyên tố cùng nhau
a) n+2 và n+3
b) 2n+3 và 3n+5
a: Gọi d=ƯCLN(n+3;n+2)
=>n+3-n-2 chia hết cho d
=>1 chia hết cho d
=>d=1
=>n+2 và n+3 là hai số nguyên tố cùng nhau
b: Gọi d=ƯCLN(2n+3;3n+5)
=>6n+9-6n-10 chia hết cho d
=>-1 chia hết cho d
=>d=1
=>2n+3 và 3n+5là hai số nguyên tố cùng nhau
Chứng minh rằng với mọi số tự nhiên n, các số sau đây là hai số nguyên tố cùng nhau:
n + 2 và n + 3
Đặt UCLN ( n+2; n+3 ) = d
=> n + 2 chia hết cho d ; n + 3 chia hết cho d
=> n + 3 - n - 2 chia hết cho d
=> 1 chia hết cho d
=> d = 1
7A. Chứng minh rằng: Với mọi số tự nhiên n, các số sau là các số nguyên tố cùng nhau:
a) n+1; n+2
b) 2n + 2; 2n + 3
c) 2n + 1; n+1
d) n + 1; 3n +4
a: \(d=UCLN\left(n+1;n+2\right)\)
\(\Leftrightarrow n+2-n-1⋮d\)
hay d=1
b: \(d=UCLN\left(2n+2;2n+3\right)\)
\(\Leftrightarrow2n+3-2n-2⋮d\)
hay d=1
7A. Chứng minh rằng: Với mọi số tự nhiên n, các số sau là các số nguyên tố cùng nhau:
a) n+1; n+2
b) 2n + 2; 2n + 3
c) 2n + 1; n+1
d) n + 1; 3n +4
k hộ mik nhé

TL


 k hộ mik
k hộ mik
Hoktot~
a: \(d=UCLN\left(n+1;n+2\right)\)
\(\Leftrightarrow n+2-n-1⋮d\)
hay d=1
b: \(d=UCLN\left(2n+2;2n+3\right)\)
\(\Leftrightarrow2n+3-2n-2⋮d\)
hay d=1