Tìm tập xác định D của hàm số y = ln ( x 2 - 3 x )
A. D = (0;3)
B. D = [0;3]
C. D = (-∞;0)∪(3;+∞)
D. D = (-∞;0)∪[3;+∞)
Tìm tập xác định D của hàm số y = l n ( 1 - x ) 2
![]()
![]()
![]()
![]()
Tìm tập xác định D của hàm số y = ln ( x - 1 )
![]()
![]()
![]()
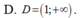
Tập xác định D của hàm số y = ln x + 2 là
A. D = [ 2 ; + ∞ )
B. D = [ e 2 ; + ∞ )
C. D = [ 1 e 2 ; + ∞ )
D. D = [ ln 2 ; + ∞ )
Chọn C.
Phương pháp: Viết điều kiện xác định và giải điều kiện đó.

Tập xác định D của hàm số y = [ l n ( x - 2 ) ] π là
![]()
![]()
![]()
![]()
Tìm tập xác định D của hàm số y = l n ( 2 x 2 - 5 x + 2 )
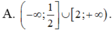
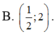
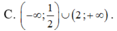
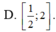
Tìm tập xác định của các hàm số sau:
a) \(y = \sqrt {{4^x} - {2^{x + 1}}} \)
b) \(y = \ln (1 - \ln x)\).
\(a,4^x-2^{x+1}\ge0\\ \Leftrightarrow2^{x+1}\le2^{2x}\\ \Leftrightarrow x+1\le2x\\ \Leftrightarrow x\ge1\)
Tập xác định của hàm số là D = \([1;+\infty)\)
\(b,\left\{{}\begin{matrix}x>0\\1-ln\left(x\right)>0\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x>0\\ln\left(x\right)< 1\end{matrix}\right.\\ \Leftrightarrow0< x< e\)
Tập xác định của hàm số là \(\left(0;e\right)\)
Cho hàm số y = ( x - 2 ) - 1 2 Bạn Toán tìm tập xác định của hàm số bằng cách như sau:
Bước 1: Ta có y = 1 ( x - 2 ) 1 2 = 1 x - 2
Bước 2: Hàm số xác định ⇔ x - 2 > 0 ⇔ x > 2
Bước 3: Vậy tập xác định của hàm số là D = ( 2 ; + ∞ )
Lời giải trên của bạn toán đúng hay sai? Nếu sai thì sai ở bước nào?
A. Bước 3
B. Bước 1
C. Đúng
D. Bước 2
Hàm số nào sau đây đồng biến trên tập xác định của nó?
A. \(y = {\log _{0,5}}x\).
B. \(y = {{\rm{e}}^{ - x}}\).
C. \(y = {\left( {\frac{1}{3}} \right)^x}\).
D. \(y = \ln x\).
Chọn D. Bởi vì hàm số ln x luôn luôn dương nên chắc chắn sẽ đồng biến trên TXĐ của nó
Tìm tập xác định của hàm số y = ln ( 1 - x ) 2 .
A . ( 1 ; + ∞ )
B . ( - ∞ ; 1 )
C . ℝ
D . ℝ \ { 1 }
Tìm tập xác định của hàm số y = ln ( 1 - x ) 2
A. ( 1 ; + ∞ )
B. ( - ∞ ; 1 )
C. R
D. R \ {1}