Đáp án C
Phương pháp:
Hàm số y = logaf(x) (0 < a ≠ 1) xác định khi và chỉ khi ⇔ f(x) > 0
Cách giải:
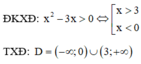
Đáp án C
Phương pháp:
Hàm số y = logaf(x) (0 < a ≠ 1) xác định khi và chỉ khi ⇔ f(x) > 0
Cách giải:
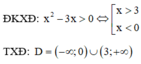
Tìm tập xác định D của hàm số y = l n ( 1 - x ) 2
![]()
![]()
![]()
![]()
Giá trị lớn nhất của hàm số y = - x 2 + 4x - 5 trên đoạn [0;3] bằng:
A. -1 B. 1
C. 2 D. 0
Giá trị lớn nhất của hàm số y = - x 2 + 4x - 5 trên đoạn [0;3] bằng:
A. -1 B. 1
C. 2 D. 0
Tìm tập xác định D của hàm số y = ln ( x - 1 )
![]()
![]()
![]()
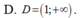
Tập xác định D của hàm số y = [ l n ( x - 2 ) ] π là
![]()
![]()
![]()
![]()
Tìm tập xác định D của hàm số y = ( 2 - x ) 1 - 3
![]()
![]()
![]()
![]()
Tìm tập xác định D của hàm số y = l n ( 2 x 2 - 5 x + 2 )
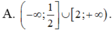
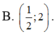
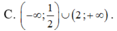
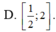
Câu 5. Tìm tập xác định D của hàm số y = ln(x2 - 3x)
A. D = (0;3)
B. D = [0;3]
C. D = (-∞;0)∪(3;+∞)
D. D = (-∞;0)∪[3;+∞)
Tìm tập xác định D của hàm số
y = ( x - 1 ) 3 .
![]()
![]()
![]()
![]()
Tìm tập xác định D của hàm số y = log 3 x + 1 x - 3
![]()
![]()
![]()
![]()