trong mặt phẳng tọa độ xOy cho F(0;1/4a) và đường thẳng (d) : y=-1/4a (a khác 0) . Gọi M(x;y) là 1 điểm thuộc mặt phẳng tọa độ. H là hình chiếu của M trên đường thẳng d
Tính \(MF^2vàMH^2\)theo x;y(tọa độ của M)
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A và B phân biệt. Biết AB song song với mặt phẳng (zOx) và không song song với hai mặt phẳng (xOy), (yOz). Tọa độ của A B ⇀ có thể là (với a,b#0)
A. (0;a;b)
B. (a;b;0)
C. (a;0;0)
D. (a;0;b).
Trong không gian với hệ tọa độ Oxyz, một vecto pháp tuyến của mặt phẳng (xOy) có tọa độ là
A. n → 0 ; - 1 ; 1
B. n → 0 ; 1 ; 1
C. n → 1 ; 1 ; 0
D. n → 0 ; 0 ; - 1
Trong mặt phẳng Oxy, cho ba điểm \(D\left( { - 1;4} \right),E\left( {0; - 3} \right),F\left( {5;0} \right)\)
a) Vẽ các điểm D, E, F trên mặt phẳng Oxy
b) Tìm tọa độ của các vectơ \(\overrightarrow {OD} ,\overrightarrow {OE} ,\overrightarrow {OF} \).
c) Vẽ và tìm tọa độ hai vectơ đơn vị và \(\overrightarrow j \)lần lượt trên hai trục tọa độ Ox và Oy
a)
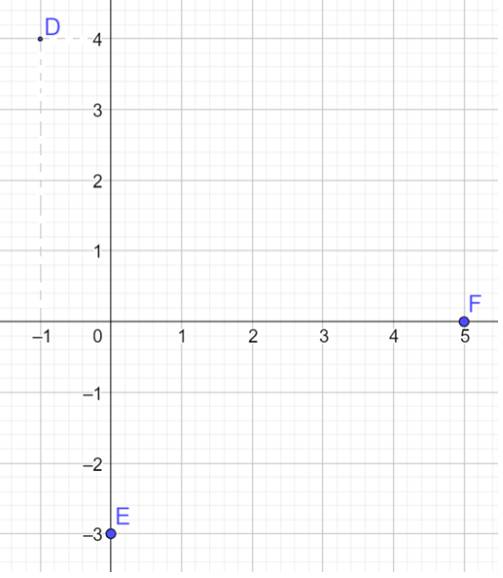
b) Vì tọa độ vectơ \(\overrightarrow {OM} \) chính là tọa độ của điểm M (với mọi M) nên ta có:
\(\overrightarrow {OD} = \left( { - 1;4} \right),\overrightarrow {OE} = \left( {0; - 3} \right),\overrightarrow {OF} = \left( {5;0} \right)\)
c)
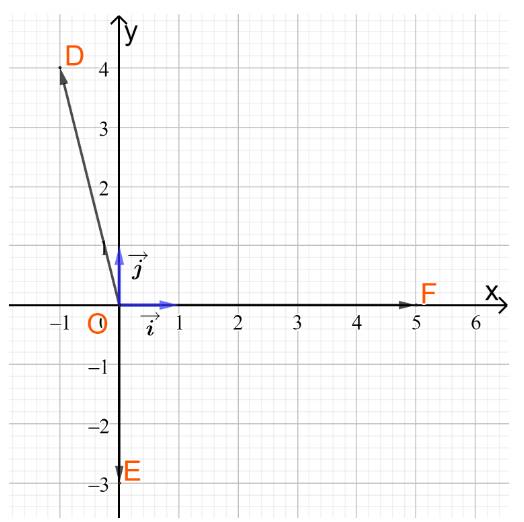
Từ hình vẽ ta có tọa độ của hai vectơ và \(\overrightarrow j \)là
và \(\overrightarrow j = (0;1)\)
Trong mặt phẳng tọa độ Oxyz, cho phương trình tổng quát của mặt phẳng (P): 2x - 6y - 8z+ 1 = 0. Một véc tơ pháp tuyến của mặt phẳng ( P) có tọa độ là
A. (-1;3;4)
B. (1;3;4)
C. (1;-3;-4)
D. (1;-3;4)
Trong hệ trục tọa độ , cho mặt phẳng (P) có phương trình 3 x - z + 1 = 0 . Véctơ pháp tuyến của mặt phẳng (P) có tọa độ là
A. (3;0;-1)
B. (3;-1;1)
C. (3;-1;0)
D. (-3;1;1)
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng: 5 x − 2 y − 3 x + 7 = 0 . Tìm tọa độ vectơ pháp tuyến n → của mặt phẳng.
A. n → = − 5 ; 2 ; − 3 .
B. n → = − 5 ; − 2 ; − 3 .
C. n → = − 5 ; 2 ; 3 .
D. n → = 5 ; 2 ; 3 .
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng P : 2 x - z + 1 = 0 . Tọa độ một véctơ pháp tuyến của mặt phẳng (P) là:
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng P : 2 x − z + 1 = 0. Tọa độ một
véctơ pháp tuyến của mặt phẳng P là
A. n → = 2 ; − 1 ; 1
B. n → = 2 ; 0 ; 1
C. n → = 2 ; 0 ; − 1
D. n → = 2 ; − 1 ; 0
Trong hệ trục tọa độ Oxyz, cho mặt phẳng (P) có phương trình 3x - z + 1 = 0 Véctơ pháp tuyến của mặt phẳng (P) có tọa độ là
A. (3;0; - 1)
B. (3; - 1;1)
C. (3; - 1;0)
D. ( - 3;1;1)